a) Xét t/giác BAD và t/giác BED có
BAD=BED (=90 độ)
ABD=EBD(BD là tia pg của ABC)
BD là cạnh chung
Do đó t/giác BAD=t/giác BED(chgn)
b)Xét t/giác ADF và t/giác EDC có
DAF=DEC(=90 độ)
AD=ED(t/giác BAD=t/giácBED)
ADF=EDC ( 2 góc đối đỉnh)
Do đó t/giác ADF=t/giác EDC(cgvgnk)
\(\Rightarrow\)AF=EC( 2 cạnh t/ứ)
Ta có BA+AF=BF
BE+EC=BC
Mà BA=BE ( t/giác BAD=t/giácBED)
AF=EC(cmt)
\(\Rightarrow\)BF=BC
Xét t/giác BDF và t/giác BDC có
BF=BC (CMT)
FBD=CDB (BD là tia pg)
BD là cạnh chung
Do đó t/giác BDF=t/giác BDC (cgc)
(giờ mình có việc r ![]() chút mình giải câu c d cho nhá)
chút mình giải câu c d cho nhá)









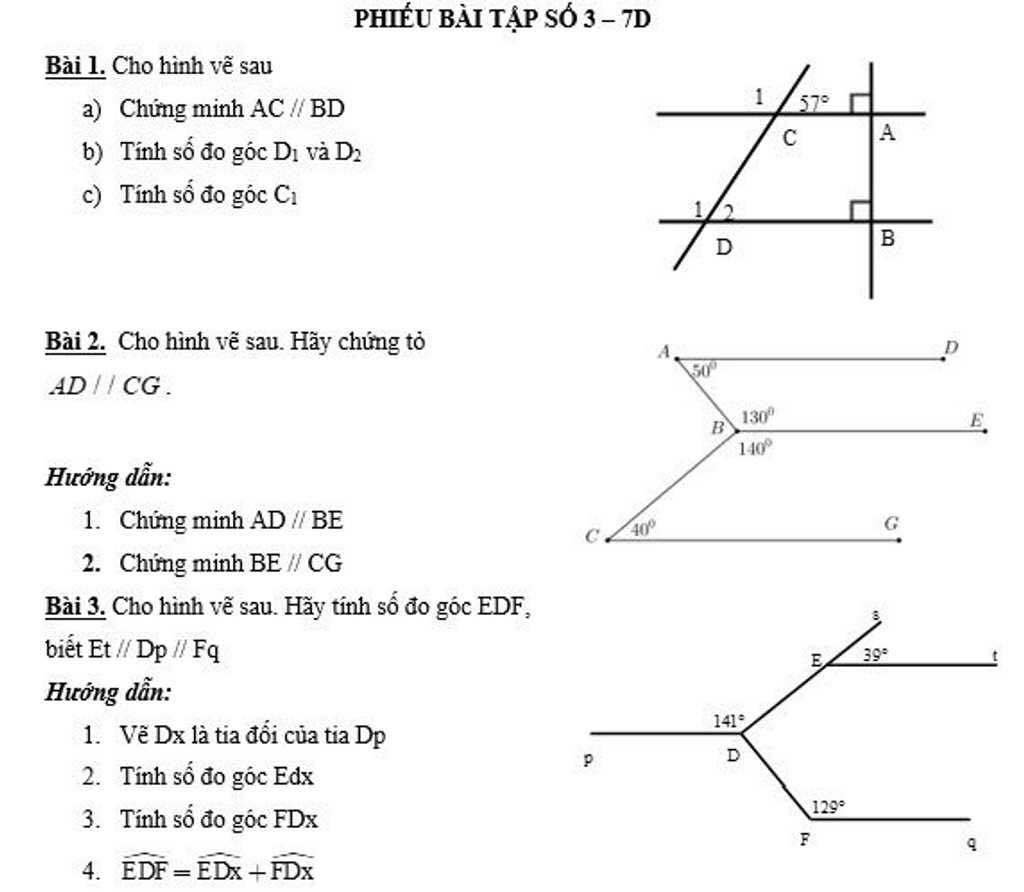 Mn giải giúp mình với mình cần gấp lắm hôm nay mình pgair nộp rồi
Mn giải giúp mình với mình cần gấp lắm hôm nay mình pgair nộp rồi

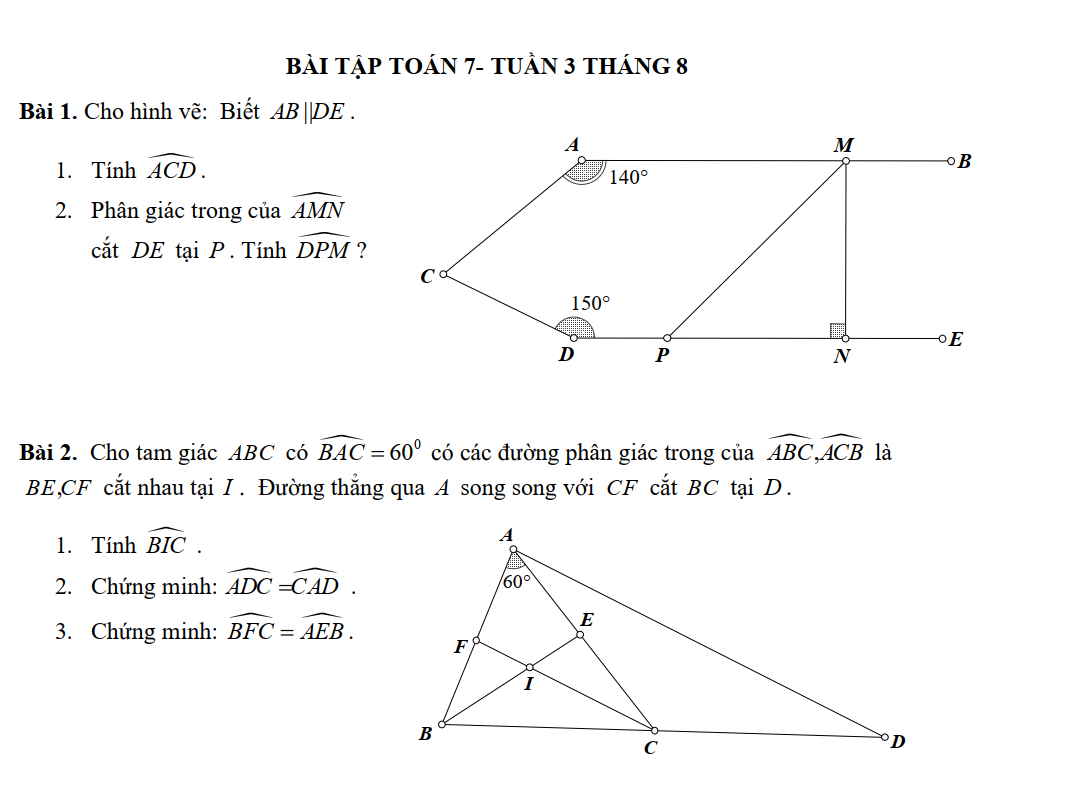


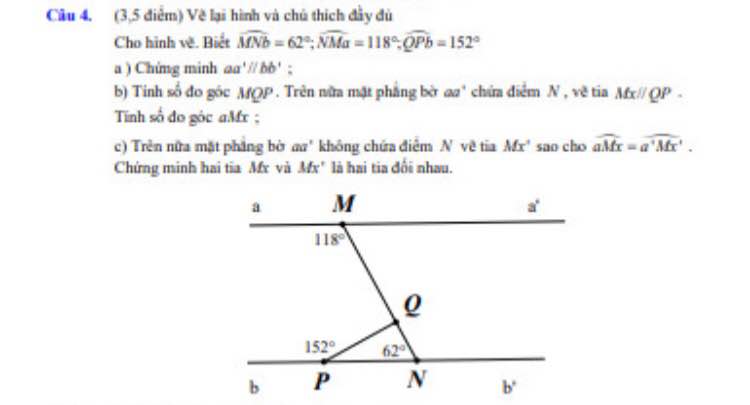

 T còn đúng 3 bài này th ạ, mg giải gấp giúp t với, 15p nx hạn nộp r
T còn đúng 3 bài này th ạ, mg giải gấp giúp t với, 15p nx hạn nộp r
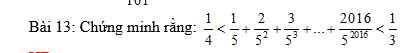 Giúp mik với ạ, chiều nay mik pk nộp r =((
Giúp mik với ạ, chiều nay mik pk nộp r =((