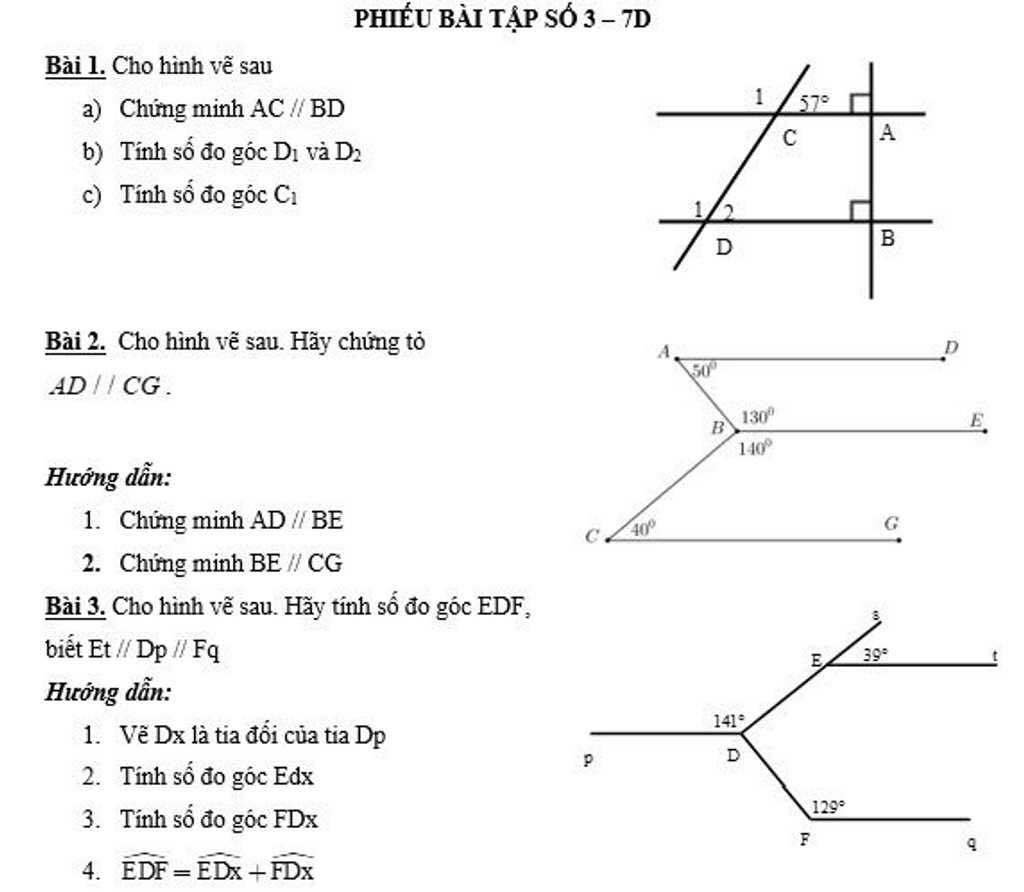
\(1,\\ a,\left\{{}\begin{matrix}AC\perp AB\\BD\perp AB\end{matrix}\right.\Rightarrow AC//BD\\ b,AC//BD\Rightarrow\widehat{D_2}=\widehat{C_1}=57^0\left(đồng.vị\right)\\ \widehat{D_2}+\widehat{D_1}=180^0\left(kề.bù\right)\Rightarrow\widehat{D_1}=180^0-57^0=123^0\\ c,AC//BD\Rightarrow\widehat{D_1}=\widehat{C_1}=123^0\left(đồng.vị\right)\)
\(2,\\ \widehat{DAB}+\widehat{ABE}=50^0+130^0=180^0\)
Mà 2 góc này ở vị trí TCP nên AD//BE (1)
\(\widehat{EBC}+\widehat{BCG}=140^0+40^0=180^0\)
Mà 2 góc này ở vị trí TCP nên BE//CG (2)
Từ (1)(2) ta được AD//CG
3.
Kẻ Dx đối Dp
Suy ra Dx//Et//Fq
\(\Rightarrow\widehat{EDx}=\widehat{sEt}=39^0\left(đồng.vị\right)\\ \widehat{FDx}=180^0-\widehat{DFq}\left(trong.cùng.phía\right)=51^0\\ \Rightarrow\widehat{EDF}=\widehat{EDx}+\widehat{FDx}=39^0+51^0=90^0\)

 Mn giải giúp mình với mình cần gấp lắm hôm nay mình pgair nộp rồi
Mn giải giúp mình với mình cần gấp lắm hôm nay mình pgair nộp rồi