Đặt \(A=\frac15+\frac{2}{5^2}+\ldots+\frac{2016}{5^{2016}}\)
=>\(5A=1+\frac25+\cdots+\frac{2016}{5^{2015}}\)
=>\(5A-A=1+\frac25+\cdots+\frac{2016}{5^{2015}}-\frac15-\frac{2}{5^2}-\ldots-\frac{2016}{5^{2016}}\)
=>\(4A=1+\frac15+\frac{1}{5^2}+\cdots+\frac{1}{5^{2015}}-\frac{2016}{5^{2016}}\)
Đặt \(B=\frac15+\frac{1}{5^2}+\cdots+\frac{1}{5^{2015}}\)
=>\(5B=1+\frac15+\cdots+\frac{1}{5^{2014}}\)
=>\(5B-B=1+\frac15+\cdots+\frac{1}{5^{2014}}-\frac15-\frac{1}{5^2}-\cdots-\frac{1}{5^{2015}}\)
=>\(4B=1-\frac{1}{5^{2015}}=\frac{5^{2015}-1}{5^{2015}}\)
=>\(B=\frac{5^{2015}-1}{5^{2015}\cdot4}\)
Ta có: \(4A=1+\frac15+\frac{1}{5^2}+\cdots+\frac{1}{5^{2015}}-\frac{2016}{5^{2016}}\)
=>\(4A=1+\frac{5^{2015}-1}{4\cdot5^{2015}}-\frac{2016}{5^{2016}}=1+\frac{5^{2016}-5-8064}{4\cdot5^{2015}}\)
=>\(4A=1+\frac14-\frac{8069}{4\cdot5^{2015}}<\frac54\)
=>\(A<\frac{5}{16}\) <5/15=1/3(2)
Ta có: \(4A=1+\frac14-\frac{8069}{4\cdot5^{2015}}\)
=>\(4A=1+\frac{5^{2015}-8069}{4\cdot5^{2015}}>1\)
=>\(A>\frac14\) (1)
Từ (1),(2) suy ra \(\frac14

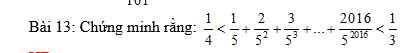 Giúp mik với ạ, chiều nay mik pk nộp r =((
Giúp mik với ạ, chiều nay mik pk nộp r =((









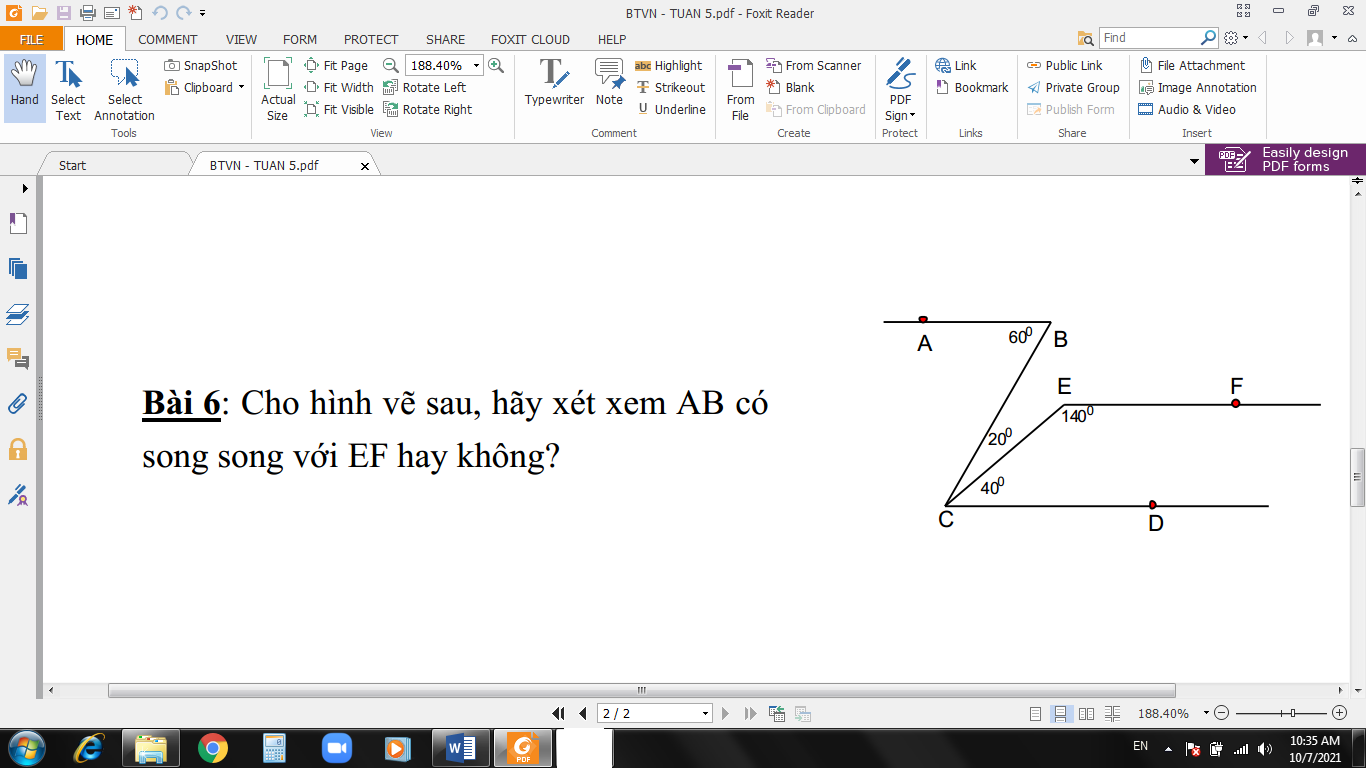 giúp mik với, chiều nộp r
giúp mik với, chiều nộp r



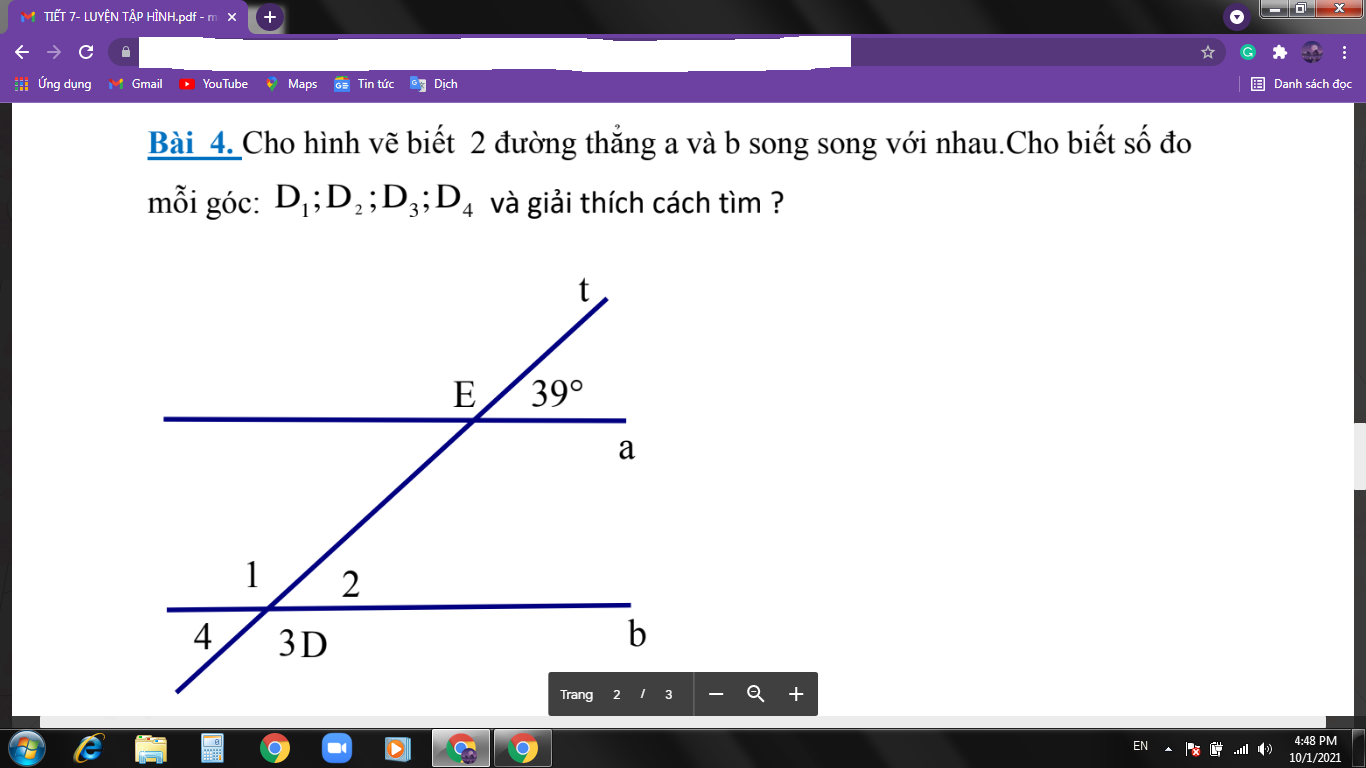 giúp mik với tối nay phải nộp rồi
giúp mik với tối nay phải nộp rồi


