Bài 4:
\(a.A=1+\dfrac{1}{5}+\dfrac{1}{5^2}+...+\dfrac{1}{5^{200}}\\ 5A=5+1+\dfrac{1}{5}+...+\dfrac{1}{5^{199}}\\ 5A-A=\left(6+\dfrac{1}{5}+...+\dfrac{1}{5^{199}}\right)-\left(1+\dfrac{1}{5}+\dfrac{1}{5^2}+...+\dfrac{1}{5^{200}}\right)\\ 4A=5-\dfrac{1}{5^{200}}\\ A=\dfrac{1}{4}\left(5-\dfrac{1}{5^{200}}\right)\\ b.B=2^{200}-2^{199}+2^{198}-2^{197}+...+2^2-2\\ 2B=2^{201}-2^{200}+2^{199}-2^{198}+...+2^3-2^2\\ 2B+B=\left(2^{201}-2^{200}+2^{199}-2^{198}+...+2^3-2^2\right)+\left(2^{200}-2^{199}+2^{198}-2^{197}+...+2^2-2\right)\\ 3B=2^{201}-2\\ B=\dfrac{1}{3}\left(2^{201}-2\right)\)
bài 3:
a: \(A=\left[\left(\dfrac{1}{7}-\dfrac{2}{3}\right)\cdot\dfrac{2}{5}\right]:\left[\left(-\dfrac{1}{3}\right)^2-1\right]\)
\(=\left[\left(\dfrac{3}{21}-\dfrac{14}{21}\right)\cdot\dfrac{2}{5}\right]:\left[\dfrac{1}{9}-1\right]\)
\(=\dfrac{-11}{21}\cdot\dfrac{2}{5}:\dfrac{-8}{9}=\dfrac{11}{21}\cdot\dfrac{2}{5}\cdot\dfrac{9}{8}=\dfrac{11}{5}\cdot\dfrac{9}{21}\cdot\dfrac{2}{8}\)
\(=\dfrac{11}{5}\cdot\dfrac{3}{7}\cdot\dfrac{1}{4}=\dfrac{33}{140}\)
b: \(B=\left(-\dfrac{1}{3}\right)^2:\dfrac{1}{2}-\left(-0,5\right)^2\left(-6\right)+\dfrac{1}{6}\)
\(=\dfrac{1}{9}\cdot2-0,25\cdot6+\dfrac{1}{6}\)
\(=\dfrac{2}{9}+\dfrac{1}{6}-\dfrac{3}{2}=\dfrac{4}{18}+\dfrac{3}{18}-\dfrac{27}{18}=\dfrac{-20}{18}=-\dfrac{10}{9}\)
c: \(C=2^3+3\cdot\left(\dfrac{2}{3}\right)^0-2^{-2}\cdot4+\left[\left(-2\right)^2:\dfrac{1}{2}\right]\cdot8\)
\(=8+3-4\cdot\dfrac{1}{4}+\left[4\cdot2\right]\cdot8\)
=11-1+64
=10+64=74
d: \(D=\dfrac{\left(-3\right)^{10}\cdot15^5}{25^3\cdot\left(-9\right)^7}=\dfrac{3^{10}\cdot3^5\cdot5^5}{5^6\cdot\left(-1\right)\cdot3^{14}}=\dfrac{-5^5}{5^6}\cdot\dfrac{3^{15}}{3^{14}}\)
\(=-\dfrac{3}{5}\)
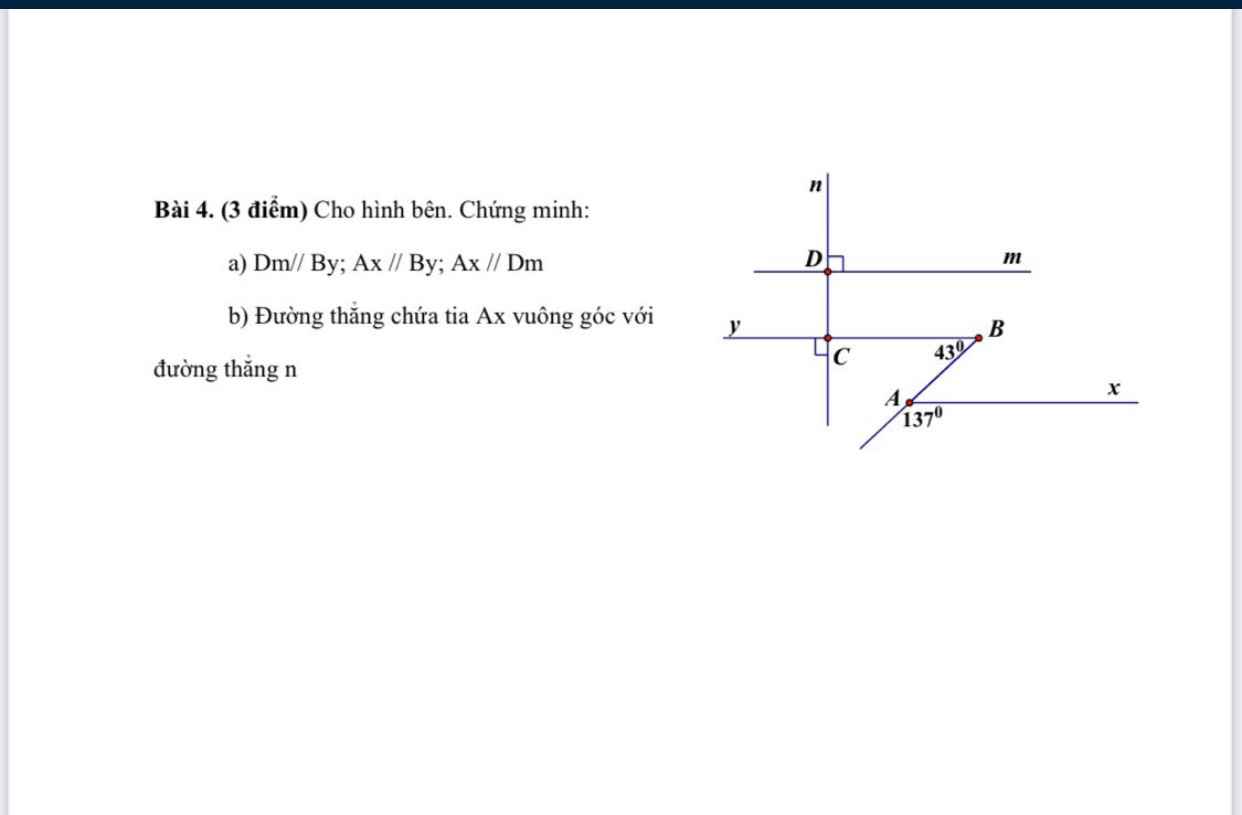
Giúp mình với ạ, mình đang cần gấp