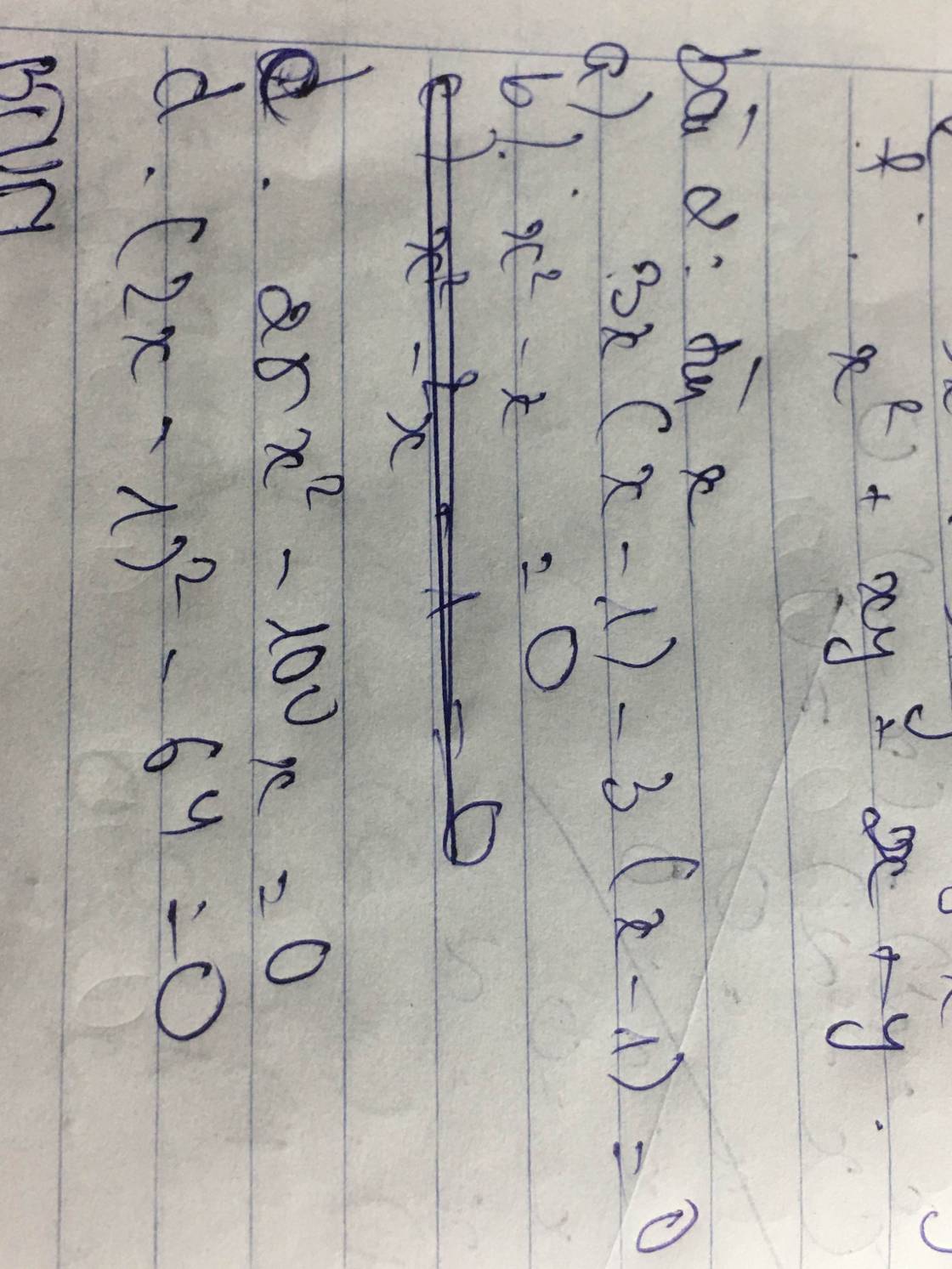Bài 5:
Ta có đa thức \(A=4x^9y^{2n}+10x^{10}y^5z^2\)
Và có đơn thức B: \(B=2x^{3n}y^4\)
Để A chia hết cho B thì: \(\dfrac{A}{B}=\dfrac{4x^9y^{2n}+10x^{10}y^5z^2}{2x^{3n}y^4}\) phải nhận giá trị nguyên:
\(\dfrac{A}{B}=\dfrac{4x^9y^{2n}}{2x^{3n}y^4}+\dfrac{10x^{10}y^5z^2}{2x^{3n}y^4}\)
\(\dfrac{A}{B}=2x^{9-3n}y^{2n-4}+5x^{10-3n}yz^2\)
Để biểu thức này nguyên thì: \(\left\{{}\begin{matrix}9-3n\ge0\\2n-4\ge0\\10-3n\ge0\end{matrix}\right.\left(n\in N\right)\)
\(\Leftrightarrow\left\{{}\begin{matrix}3n\le9\\2n\ge4\\3n\le10\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}n\le3\\n\ge2\\n\le\dfrac{10}{3}\end{matrix}\right.\)
\(\Leftrightarrow2\le n\le3\)
Mà: \(n\in N\) nên:
\(\Leftrightarrow n\in\left\{2;3\right\}\)
Vậy: ....
giúp mình với ạ, mình cần gấp lắm ạ
