Giúp mình với ạ, mình cần gấp
\(\dfrac{2x}{x+1}=\dfrac{x^2-x+8}{\left(x+1\right)\left(x-4\right)}\text{ĐKXĐ:}x\ne-1;4\)
\(\Leftrightarrow\dfrac{2x\left(x-4\right)}{\left(x+1\right)\left(x-4\right)}=\dfrac{x^2-x+8}{\left(x+1\right)\left(x-4\right)}MTC:\left(x+1\right)\left(x-4\right)\)
\(\Rightarrow2x^2-8x=x^2-x+8\)
\(\Leftrightarrow2x^2-8x-x^2+x-8=0\)
\(\Leftrightarrow x^2-7x-8=0\)
\(\Leftrightarrow x^2-8x+x-8=0\)
\(\Leftrightarrow\left(x^2-8x\right)+\left(x-8\right)=0\)
\(\Leftrightarrow x\left(x-8\right)+\left(x-8\right)=0\)
\(\Leftrightarrow\left(x-8\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-8=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=8\left(\text{nhận}\right)\\x=-1\left(\text{loại}\right)\end{matrix}\right.\)
\(\text{Vậy phương trình có tập nghiệm là }S=\left\{8\right\}\)
=>2x(x-4)=x^2-x+8
=>2x^2-8x-x^2+x-8=0
=>x^2-7x-8=0
=>(x-8)(x+1)=0
=>x=8 hoặc x=-1(loại)
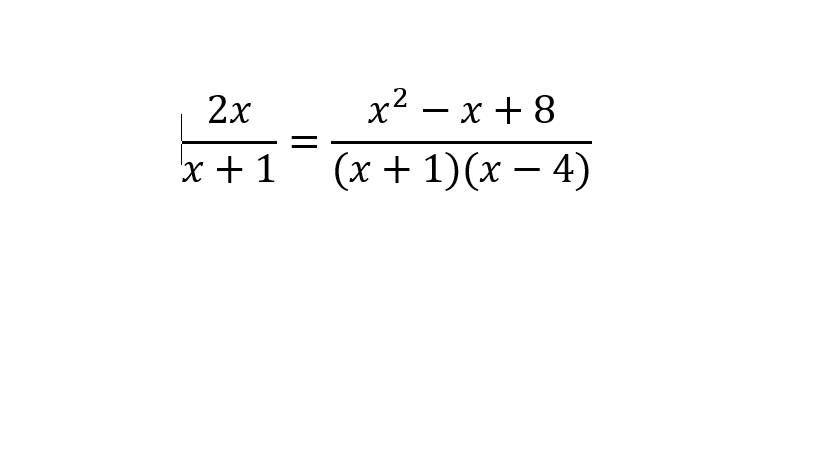giúp mình với ạ, mình cần gấp lắm ạ
