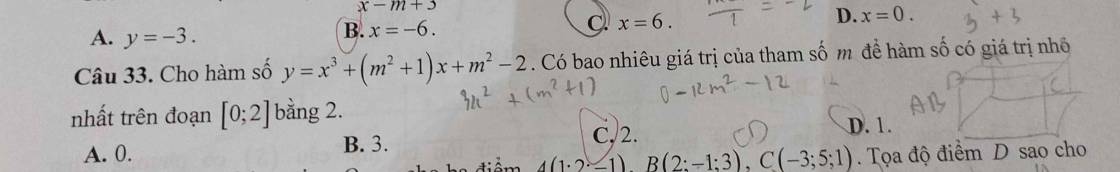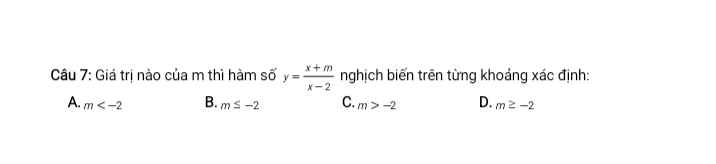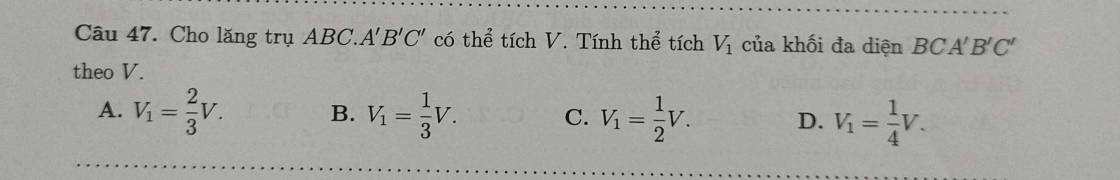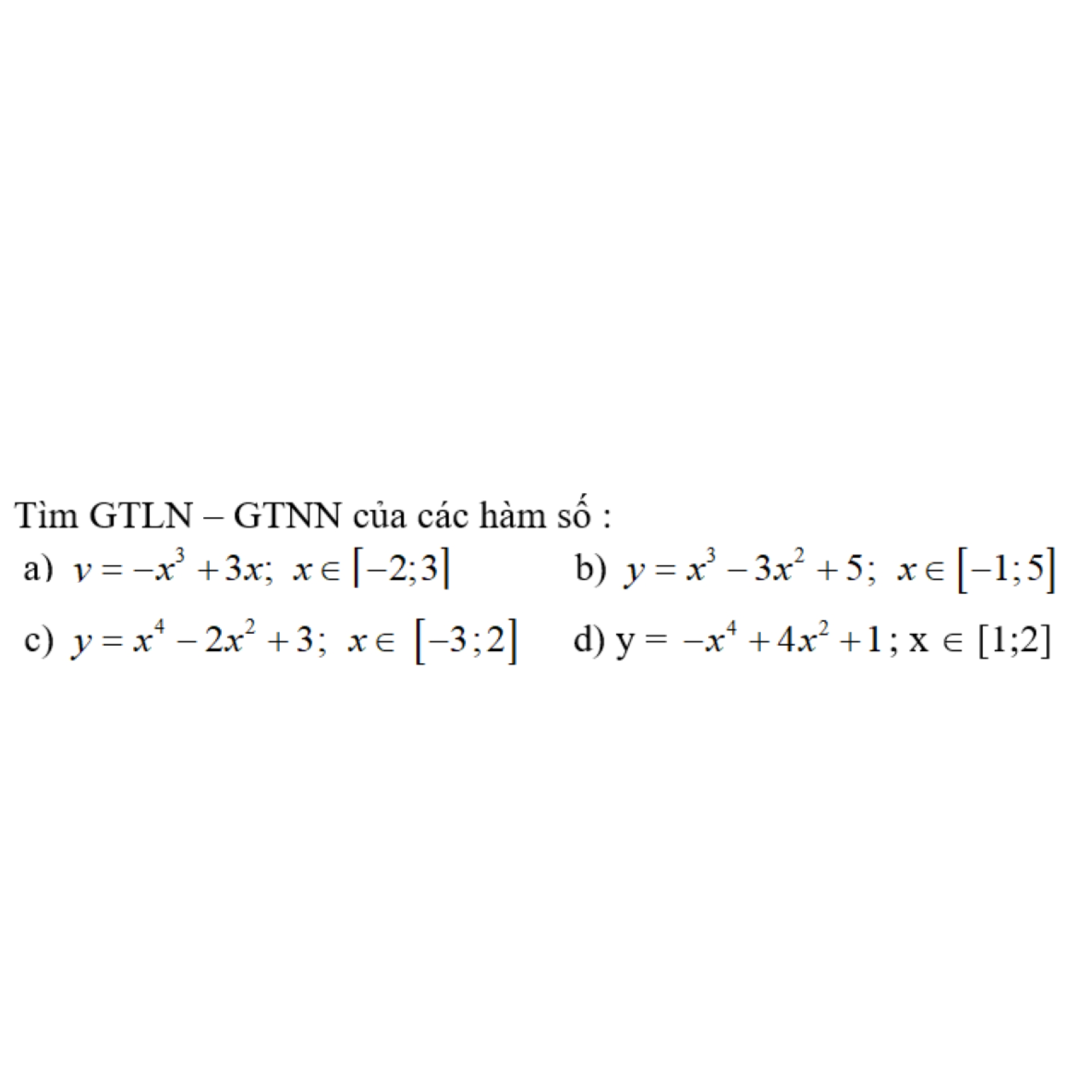Lời giải:
$y'=3x^2+m^2+1>0$ với mọi $x\in [0;2]$
$\Rightarrow$ hàm số $y$ luôn đồng biến trên $[0;2]$
$\Rightarrow y_{\min}=y(0)=m^2-2$
Để $y_{\min}=2$
$\Leftrightarrow m^2-2=2$
$\Leftrightarrow m=\pm 2$
Đáp án C.
Đúng 2
Bình luận (0)