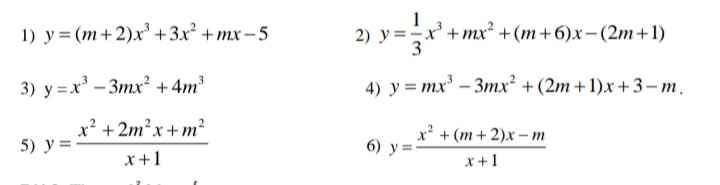Lời giải:
Để $y$ có 2 điểm cực trị thì:
$y'=3mx^2-2(m+1)x+2m-\frac{2}{3}=0$ có 2 nghiệm phân biệt.
\(\Leftrightarrow \left\{\begin{matrix} m\neq 0\\ \Delta'=(m+1)^2-3m(2m-\frac{2}{3})>0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} m\neq 0\\ -5m^2+4m+1>0\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} m\neq 0\\ (1-m)(5m+1)>0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} m\neq 0\\ \frac{-1}{5}< m< 1\end{matrix}\right.\)
Đáp án A.
Đúng 0
Bình luận (0)
