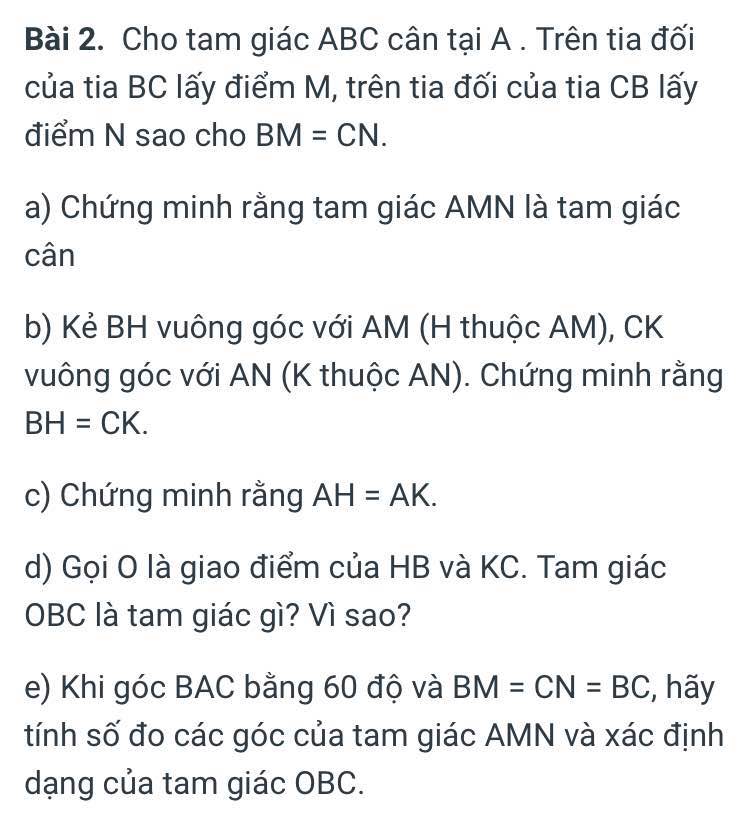
a. xét tam giác ABM và tam giác ACN, có:
AB = AC ( ABC cân )
góc ABM = góc ACN ( 2 góc ngoài của tam giác cân )
BM = CN ( gt )
Vậy tam giác ABM = tam giác ACN ( c.g.c )
b. xét tam giác vuông ABH và tam giác vuông ACK, có:
AB = AC ( ABC cân )
góc MAB = góc NAC ( tam giác ABM = tam giác ACN )
Vậy tam giác vuông ABH = tam giác vuông ACK ( cạnh huyền.góc nhọn )
=> BH = CK ( 2 cạnh tương ứng )
c. ta có: tam giác vuông ABH = tam giác vuông ACK
=> AH = AK ( 2 cạnh tương ứng )
d. ta có: góc OBC = góc OCB
=> tam giác OBC cân tại O
e. ta có AB = AC mà A = 60 độ
=> ABC là tam giác đều
Mà BM = CN = BC , BC lại = AB
=> BM = CN = AB
Mà góc AMB = góc ANC ( cmt )
=> tam giác AMN là tam giác đều ( BM = CN và góc AMB = góc ANC )
Tham khảo:
a) tam giác ABC cân
=> góc ABC=góc ACB
góc MBA+góc ABC=180độ (kề bù)
góc NCA+góc ACB=180độ(kề bù)
=> góc ABM=góc ACN
xét 2 tam giác ABM và ACN có:
AB=AC(tam giác ABC cân )
góc ABM=góc ACN(chứng minh trên)
BM=CN(gt)
=> 2 tam giác ABM=ACN(c.g.c)
=> AM=AN(2 cạnh tương ứng)
=> tam giác AMN cân ở A
b) tam giác AMN cân ở A
=> góc M=góc N
xét 2 tam giác MHB và NKC có:
góc MHB=góc NKC(=90độ)
MB=NC(gt)
góc M =góc N(chứng minh trên)
=> 2 tam giác MHB=NKC(cạnh huyền - góc nhọn)
=> BH=CK(2 cạnh tương ứng)
c) ta có : AM=AN (theo a)
HM=KN (tam giác MHB=tam giác NKC)
AM = AH+HM
AN= AK+ KN
=> AH= AK
d) tam giác MHB=tam giác NKC(theo b)
=> góc HBM=góc KCN(2 góc tương ứng)
góc HBM=góc OBC(đối đỉnh)
góc KCN=góc OCB(đối đỉnh)
=> góc OBC=góc OCB
=> tam giác OBC cân ở O
e) tam giác ABC có AB=AC ; góc BAC=60độ
=> tam giác ABC đều
=> AB=AC=BC
mà BC=BM(gt)
=> BM=AB
=>tam giác ABM cân ở B
góc ABC + góc ABM=180độ (kề bù)
=> góc ABM =180độ - góc ABC
=180độ-60độ
=120độ
tam giác ABC cân ở B
=> góc BAM=góc BMA =(180độ-góc ABM) / 2=180−120/2=60/2=30 độ
vậy góc AMN=30độ