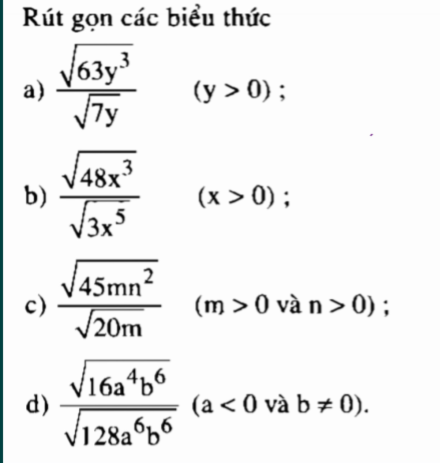a: ĐKXĐ: x>0 và y>0
b: \(P=\dfrac{x+\sqrt{xy}-y+\sqrt{xy}}{\sqrt{x}+\sqrt{y}}:\left(\dfrac{x}{\sqrt{y}\left(\sqrt{x}+\sqrt{y}\right)}-\dfrac{y}{\sqrt{x}\left(\sqrt{x}-\sqrt{y}\right)}+\dfrac{x+y}{\sqrt{xy}}\right)\)
\(=\dfrac{x+2\sqrt{xy}-y}{\sqrt{x}+\sqrt{y}}:\dfrac{x\sqrt{x}\left(\sqrt{x}-\sqrt{y}\right)-y\sqrt{y}\left(\sqrt{x}+\sqrt{y}\right)+x^2-y^2}{\sqrt{xy}\left(x-y\right)}\)
\(=\dfrac{x+2\sqrt{xy}-y}{\sqrt{x}+\sqrt{y}}\cdot\dfrac{\sqrt{xy}\left(x-y\right)}{x^2-x\sqrt{xy}-y\sqrt{xy}-y^2+x^2-y^2}\)
\(=\dfrac{x+2\sqrt{xy}-y}{1}\cdot\dfrac{\sqrt{xy}\left(\sqrt{x}-\sqrt{y}\right)}{2x^2-2y^2-\left(x+y\right)\sqrt{xy}}\)
\(=\dfrac{x+2\sqrt{xy}-y}{1}\cdot\dfrac{\sqrt{xy}\left(\sqrt{x}-\sqrt{y}\right)}{\left(x+y\right)\left(2x-2y-\sqrt{xy}\right)}\)
\(=\dfrac{\sqrt{xy}\left(\sqrt{x}-\sqrt{y}\right)\left(x+2\sqrt{xy}-y\right)}{\left(x+y\right)\left(2x-2y-\sqrt{xy}\right)}\)