\(ĐK:x\ge0\\ P=\dfrac{3\sqrt{x}-1}{\sqrt{x}+1}=\sqrt{x}\\ \Leftrightarrow\sqrt{x}.\left(\sqrt{x}+1\right)=3\sqrt{x}-1\\ \Leftrightarrow x+\sqrt{x}-3\sqrt{x}+1=0\\ \Leftrightarrow x-2\sqrt{x}+1=0\\ \Leftrightarrow\left(\sqrt{x}-1\right)^2=0\\ \Leftrightarrow\sqrt{x}-1=0\\ \Leftrightarrow\sqrt{x}=1\\ \Leftrightarrow x=1^2=1\\ \Rightarrow Chọn.A\)
Câu `22:`
Ta có: `[\sqrt{x}+1]/[\sqrt{x}-2]=[\sqrt{x}-1]/2`
`<=>2\sqrt{x}+2=x-\sqrt{x}-2\sqrt{x}+2`
`<=>x-5\sqrt{x}=0`
`<=>[(\sqrt{x}=0),(\sqrt{x}=5):}<=>[(x=0),(x=25):} ->\bb C`








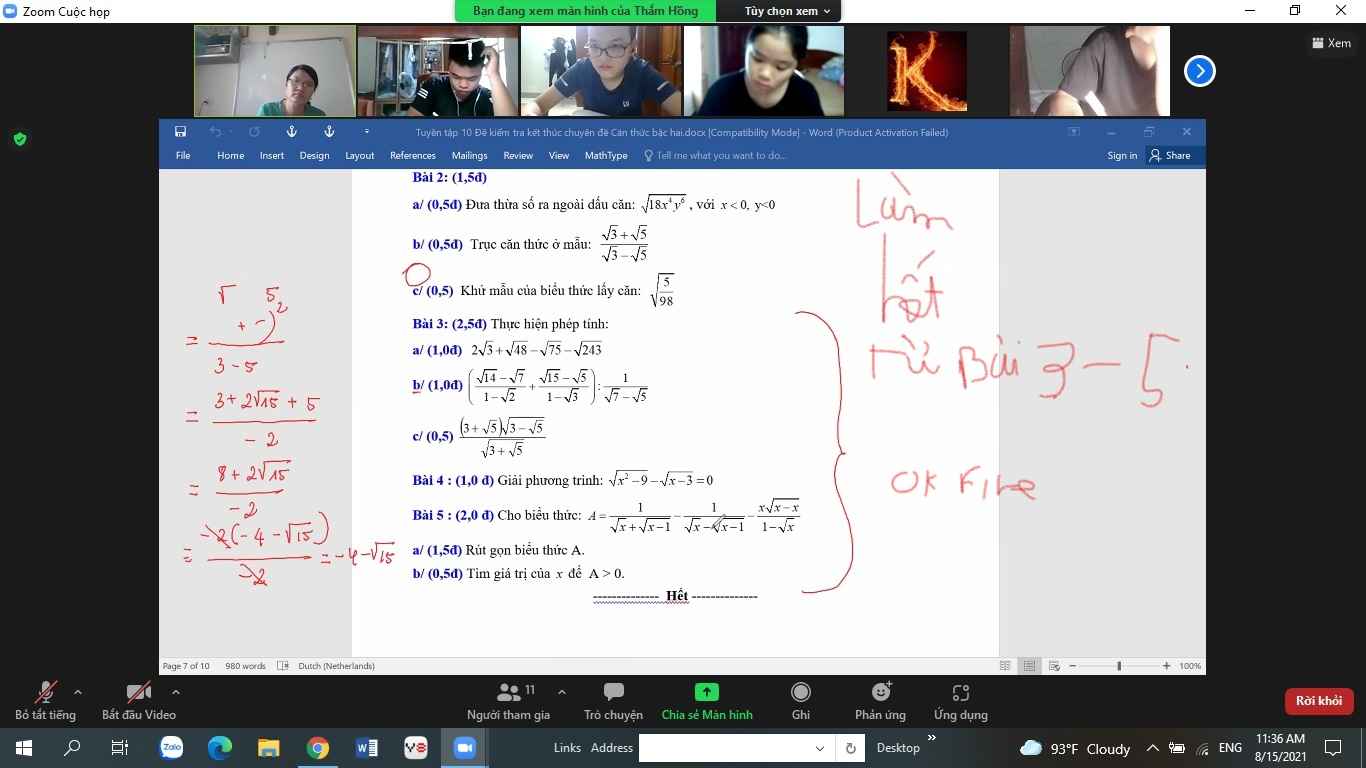





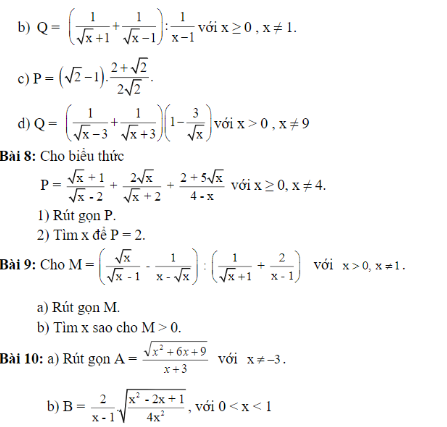



 Mn giúp có thể giúp mình câu C bài 4 và bài 5 được ko ạ, giải chi tiết 1 chút với ạ. Mình cảm ơn
Mn giúp có thể giúp mình câu C bài 4 và bài 5 được ko ạ, giải chi tiết 1 chút với ạ. Mình cảm ơn






