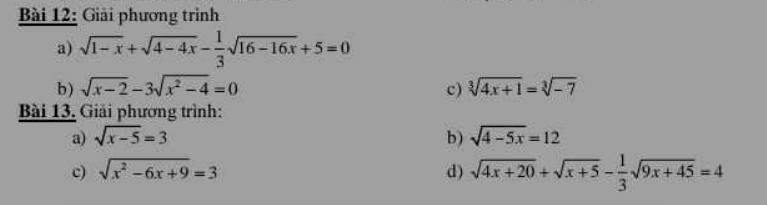Bài 13:
a) \(\sqrt{x-5}=3\) (ĐK: \(x\le5\) )
\(\Leftrightarrow x-5=3^2\)
\(\Leftrightarrow x-5=9\)
\(\Leftrightarrow x=14\) (tm)
Vậy: ....
b) \(\sqrt{4-5x}=12\) (ĐK: \(x\ge\dfrac{4}{5}\))
\(\Leftrightarrow\sqrt{4-5x}=12\)
\(\Leftrightarrow4-5x=12^2\)
\(\Leftrightarrow4-5x=144\)
\(\Leftrightarrow-5x=140\)
\(\Leftrightarrow x=\dfrac{140}{-5}=-28\) (tm)
Vậy: ...
c) \(\sqrt{x^2-6x+9}=3\)
\(\Leftrightarrow\sqrt{\left(x-3\right)^2}=3\)
\(\Leftrightarrow\left|x-3\right|=3\)
TH1: \(\left|x-3\right|=-\left(x-3\right)\) với \(x-3< 0\Leftrightarrow x< 3\)
Pt trở thành:
\(-\left(x-3\right)=3\) (ĐK: \(x< 3\) )
\(\Leftrightarrow-x+3=3\)
\(\Leftrightarrow-x=0\)
\(\Leftrightarrow x=0\left(tm\right)\)
TH2: \(\left|x-3\right|=x-3\) với \(x-3\ge0\Leftrightarrow x\ge3\)
Pt trở thành:
\(x-3=3\) (ĐK: \(x\ge3\) )
\(\Leftrightarrow x=6\left(tm\right)\)
Vậy: ....
d) \(\sqrt{4x+20}+\sqrt{x+5}-\dfrac{1}{3}\sqrt{9x+45}=4\) (ĐK: \(x\ge-5\) )
\(\Leftrightarrow\sqrt{4\left(x+5\right)}+\sqrt{x+5}-\dfrac{1}{3}\sqrt{9\left(x+5\right)}=4\)
\(\Leftrightarrow2\sqrt{x+5}+\sqrt{x+5}-\sqrt{x+5}=4\)
\(\Leftrightarrow2\sqrt{x-5}=4\)
\(\Leftrightarrow\sqrt{x-5}=2\)
\(\Leftrightarrow x-5=4\)
\(\Leftrightarrow x=9\left(tm\right)\)
Vậy: ...