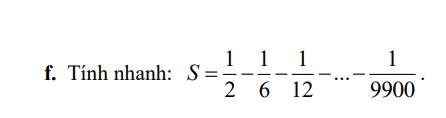\(S=\dfrac{1}{2}-\dfrac{1}{6}-\dfrac{1}{12}-...-\dfrac{1}{9900}\)
\(=\dfrac{1}{2}-\left(\dfrac{1}{6}+\dfrac{1}{12}+...+\dfrac{1}{9900}\right)\)
\(=\dfrac{1}{2}-\left(\dfrac{1}{2\cdot3}+\dfrac{1}{3\cdot4}+...+\dfrac{1}{99\cdot100}\right)\)
\(=\dfrac{1}{2}-\left(\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{99}-\dfrac{1}{100}\right)\)
\(=\dfrac{1}{2}-\left(\dfrac{1}{2}-\dfrac{1}{100}\right)\)
\(=\dfrac{1}{2}-\dfrac{1}{2}+\dfrac{1}{100}=\dfrac{1}{100}\)