11.
1)
Ta có :
ABCD là hình bình hành \(\Rightarrow\) AB // DC;AD // BC;AB = DC;AD = BC
Mà : E \(\in\) AB ; F \(\in\) DC
\(\Rightarrow\) AE // DF ; BE // CF
2)
Ta có :
AB = DC (cmt) (1)
AE=DF (gt) (2)
Từ (1) và (2) \(\Rightarrow\) BE = CF
3)
Ta có :
AE // DF (gt)
AE = DF (cmt)
\(\Rightarrow\) Tứ giác AEFD là hình bình hành
4)
Ta có :
BE // CF (cmt)
BE=CF (cmt)
\(\Rightarrow\) Tứ giác BEFC là Hình Bình Hành
12.
1)
Ta có:
Tứ Giác ABCD là Hình Bình Hành
\(\Rightarrow\) AB // DC; AD // BC; AB = DC; AD = BC
Mà :
E \(\in\) AB (gt) (1)
F \(\in\) DC (gt) (2)
Từ (1) và (2) \(\Rightarrow\) AE // CF; EB // DF
2)
Ta có :
AB = DC (cmt)
AE = FC (gt)
\(\Rightarrow\) BE = DF
3)
Ta có :
Tứ Giác AECF là Hình Bình Hành\(\left\{{}\begin{matrix}AE=CF\left(gt\right)\\AE//CF\left(cmt\right)\end{matrix}\right.\)
4)
Ta có :
Tứ Giác BEDF là Hình Bình Hành \(\left\{{}\begin{matrix}BE=DF\left(cmt\right)\\BE//DF\left(cmt\right)\end{matrix}\right.\)
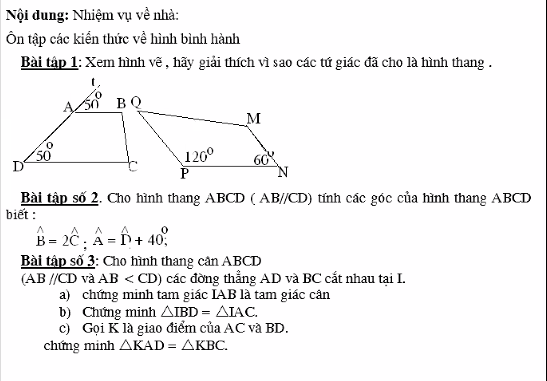
help mik vs mai phải nộp r;-;
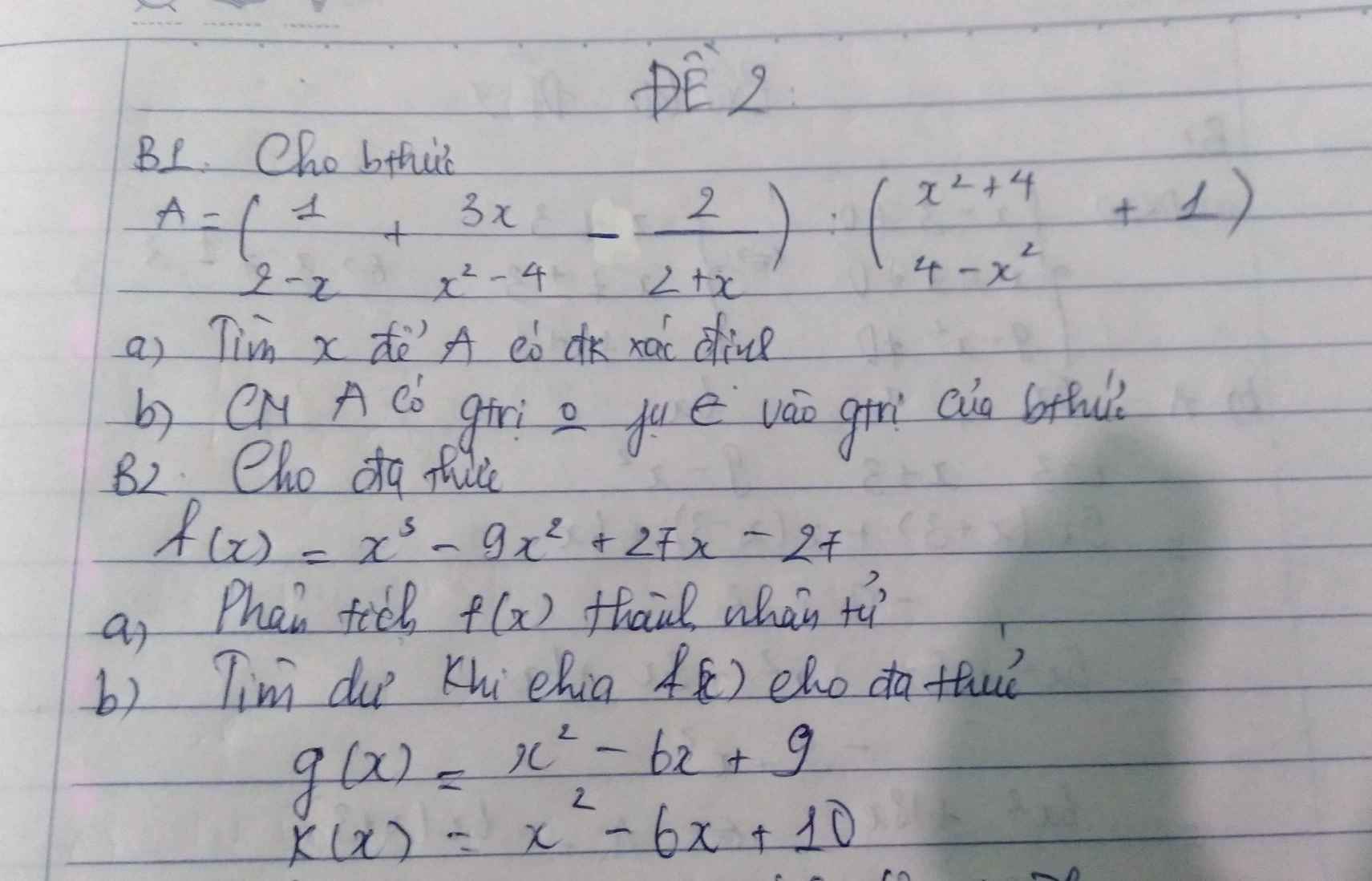
AI GIÚP MIK VS Ạ. MAI MIK IK HỌC R Ạ 
