Để hệ có nghiệm duy nhất thì \(\dfrac{1}{m}\ne\dfrac{m}{1}\)
=>\(m^2\ne1\)
=>\(m\notin\left\{1;-1\right\}\left(1\right)\)
\(\left\{{}\begin{matrix}x+my=m+1\\mx+y=3m-1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=m+1-my\\m\left(m+1-my\right)+y=3m-1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=m+1-my\\m^2+m-m^2y+y=3m-1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=m+1-my\\m^2+m+y\left(1-m^2\right)=3m-1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=m+1-my\\y\left(1-m^2\right)=3m-1-m^2-m=-m^2+2m-1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=\dfrac{-m^2+2m-1}{1-m^2}=\dfrac{m^2-2m+1}{m^2-1}=\dfrac{\left(m-1\right)^2}{\left(m-1\right)\left(m+1\right)}=\dfrac{m-1}{m+1}\\x=m+1-m\cdot\dfrac{m-1}{m+1}=\dfrac{\left(m+1\right)^2-m\left(m-1\right)}{m+1}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=\dfrac{m-1}{m+1}\\x=\dfrac{m^2+2m+1-m^2+m}{m+1}=\dfrac{3m+1}{m+1}\end{matrix}\right.\)
Để x,y đều là các số nguyên thì \(\left\{{}\begin{matrix}3m+1⋮m+1\\m-1⋮m+1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3m+3-2⋮m+1\\m+1-2⋮m+1\end{matrix}\right.\)
=>\(-2⋮m+1\)
=>\(m+1\in\left\{1;-1;2;-2\right\}\)
=>\(m\in\left\{0;-2;1;-3\right\}\)
Kết hợp (1) ta được: \(m\in\left\{0;-2;-3\right\}\)

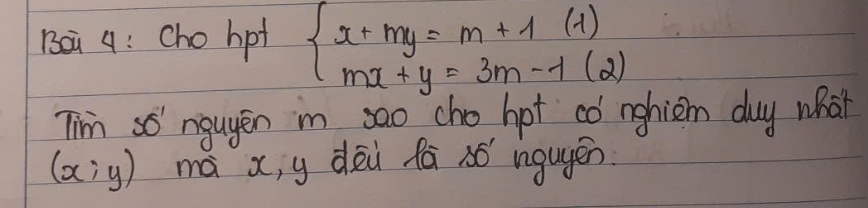 giúp mik vs cần gấp ạ
giúp mik vs cần gấp ạ














 giúp câu c vs ạ,mik cần gấp
giúp câu c vs ạ,mik cần gấp