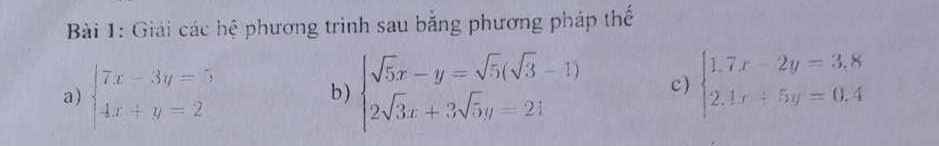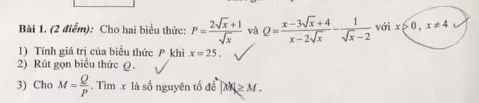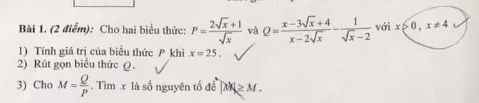\(a)\left\{{}\begin{matrix}7x-3y=5\\4x+y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}7x-3y=5\\12x+3y=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}21x=11\\4x+y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{11}{21}\\\dfrac{44}{21}+y=2\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{11}{21}\\y=2-\dfrac{44}{21}=-\dfrac{2}{21}\end{matrix}\right.\\ c,\left\{{}\begin{matrix}1,7x-2y=3,8\\2,4x+5y=0,4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}17x-20y=38\\24x+50y=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{17}{2}x-10y=19\\\dfrac{24}{5}x+10y=\dfrac{4}{5}\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}\dfrac{133}{10}x=\dfrac{99}{5}\\24x+50y=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{99}{5}:\dfrac{133}{10}=\dfrac{198}{133}\\\dfrac{4752}{133}+50y=4\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{198}{133}\\50y=4-\dfrac{4752}{133}=-\dfrac{4220}{133}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{198}{133}\\y=\dfrac{-4220}{133}:50=-\dfrac{422}{665}\end{matrix}\right.\)
a: \(\left\{{}\begin{matrix}7x-3y=5\\4x+y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=2-4x\\7x-3\left(2-4x\right)=5\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=2-4x\\7x-6+12x=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}19x=11\\y=2-4x\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{11}{19}\\y=2-4\cdot\dfrac{11}{19}=2-\dfrac{44}{19}=-\dfrac{6}{19}\end{matrix}\right.\)
b: \(\left\{{}\begin{matrix}x\sqrt{5}-y=\sqrt{5}\left(\sqrt{3}-1\right)\\2\sqrt{3}x+3\sqrt{5}\cdot y=21\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=x\sqrt{5}-\sqrt{5}\left(\sqrt{3}-1\right)\\2\sqrt{3}\cdot x+3\sqrt{5}\cdot\sqrt{5}\left(x-\sqrt{3}+1\right)=21\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=x\sqrt{5}-\sqrt{5}\left(\sqrt{3}-1\right)\\2\sqrt{3}x+15x-15\sqrt{3}+15=21\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=\sqrt{5}\left(x-\sqrt{3}+1\right)\\x\left(15+2\sqrt{3}\right)=21-15+15\sqrt{3}=15\sqrt{3}+6\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=\sqrt{5}\left(x-\sqrt{3}+1\right)\\x=\sqrt{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\sqrt{5}\\x=\sqrt{3}\end{matrix}\right.\)
c: \(\left\{{}\begin{matrix}1,7x-2y=3,8\\2,4x+5y=0,4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2y=1,7x-3,8\\2,4x+2,5\cdot2y=0,4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=\dfrac{1,7x-3,8}{2}\\2,4x+2,5\left(1,7x-3,8\right)=0,4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=\dfrac{1,7x-3,8}{2}\\2,4x+4,25x=0,4+2,5\cdot3,8=9,9\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}6,65x=9,9\\y=\dfrac{1,7x-3,8}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{198}{133}\\y=\dfrac{1,7\cdot\dfrac{198}{133}-3,8}{2}=-\dfrac{422}{665}\end{matrix}\right.\)
\(b)\left\{{}\begin{matrix}\sqrt{5}x-y=\sqrt{5}\left(\sqrt{3}-1\right)\\2\sqrt{3}x+3\sqrt{5}y=21\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}15x-3\sqrt{5}y=15\left(\sqrt{3}-1\right)\\2\sqrt{3}x+3\sqrt{5}y=21\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}\left(2\sqrt{3}+15\right)x=15\sqrt{3}-15+21=15\sqrt{3}+6\\\sqrt[]{5}x-y=\sqrt{5}\left(\sqrt{3}-1\right)\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{15\sqrt{3}+6}{2\sqrt{3}+15}=\sqrt{3}\\\sqrt{15}-y=\sqrt{15}-\sqrt{5}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\sqrt{3}\\y=\sqrt{15}-\sqrt{15}+\sqrt{5}=\sqrt{5}\end{matrix}\right.\)