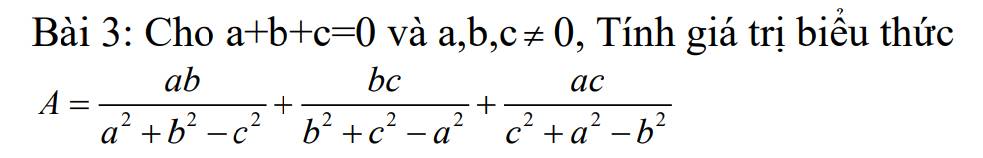3:
a^3+b^3+c^3=3abc
=>a^3+b^3+c^3-3abc=0
=>(a+b)^3+c^3-3ab(a+b)-3abc=0
=>(a+b+c)(a^2+2ab+b^2-ac-bc+c^2-3ab)=0
=>(a+b+c)[2a^2+2b^2+2c^2-2ab-2ac-2bc]=0
=>(a+b+c)[(a-b)^2+(b-c)^2+(a-c)^2]=0
=>a=b=c hoặc a+c+b=0
Bài 1
\(a,\left(a+b\right)^2-\left(a-b\right)^2=4ab\\ VT=a^2+2ab+b^2-a^2+2ab-b^2\\ =4ab=VP\\ b,a^3+b^3=\left(a+b\right)^3-3ab\left(a+b\right)\\ VP=a^3+3a^2b+3ab^2+b^3-3a^2b-3ab^2\\ =a^3+b^3=VT\)