`4,`
`a,`
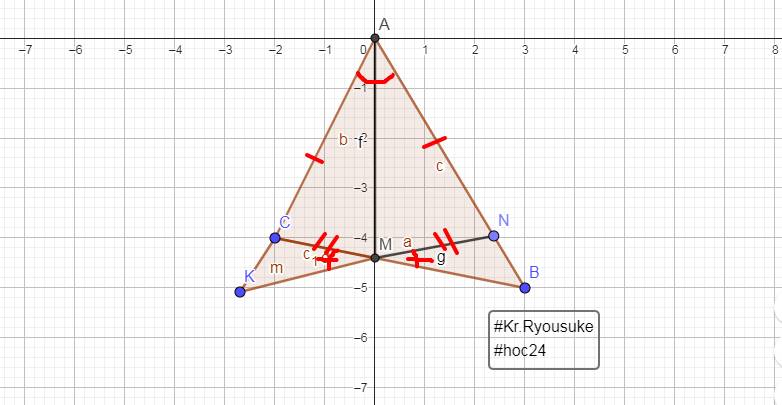
Xét `\Delta ACM` và `\Delta ANM`:
`\text {AC = AN (gt)}`
$\widehat {CAM} = \widehat {NAM} (\text {tia phân giác} \widehat {CAN})$
`\text {AM chung}`
`=> \Delta ACM = \Delta ANM (c-g-c)`
`-> \text {MC = MN (2 cạnh tương ứng)}`
`b,`
Vì `\Delta ACM = \Delta ANM (a)`
`->` $\widehat {ACM} = \widehat {ANM} (\text {2 góc tương ứng})`
Ta có: \(\left\{{}\begin{matrix}\widehat{\text{ACM}}+\widehat{\text{KCM}}=180^0\left(\text{kề bù}\right)\\\widehat{\text{ANM}}+\widehat{\text{BNM}}=180^0\left(\text{kề bù}\right)\end{matrix}\right.\)
Mà \(\widehat{\text{ACM}}=\widehat{\text{ANM}}\)
`->`\(\widehat{\text{KCM}}=\widehat{\text{BNM}}\)
Xét `\Delta MCK` và `\Delta MNB`:
\(\widehat{\text{KCM}}=\widehat{\text{BNM}}\left(\text{CMT}\right)\)
\(\text{MC = MN (a)}\)
\(\widehat{\text{CMK}}=\widehat{\text{NMB}}\left(\text{đối đỉnh}\right)\)
`=> \Delta MCK = \Delta MNB (g-c-g)`.