`8,`
`a,`
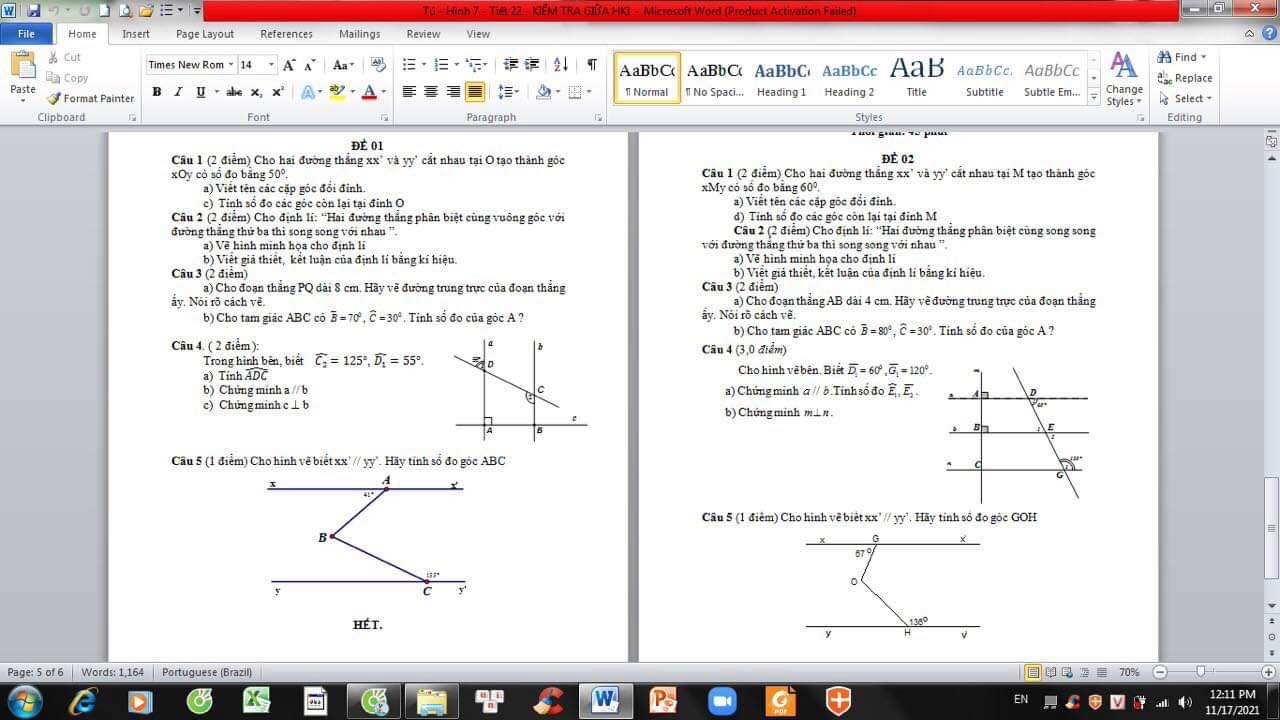
`M(x)=A(x)+B(x)`
`M(x)=(x^3-3x^2+5x+3)+(-x^3+x^2+x^4-5x+3)`
`= x^3-3x^2+5x+3-x^3+x^2+x^4-5x+3`
`= x^4+ (x^3-x^3)+(-3x^2+x^2)+(5x-5x)+(3+3)`
`= x^4-2x^2+6`
`N(x)=A(x)-B(x)`
`N(x)=(x^3-3x^2+5x+3)-(-x^3+x^2+x^4-5x+3)`
`= x^3-3x^2+5x+3+x^3-x^2-x^4+5x-3`
`= x^4+(x^3+x^3)+(-3x^2-x^2)+(5x+5x)+(3-3)`
`= x^4+2x^3-4x^2+10x`
`b,`
Thay `x=1`
`M(1)=1^4-2*1^2+6=1-2+6=-1+6=5`
`-> x=1` không phải là nghiệm của đa thức.
`c,`
`M(x)=x^4-2x^2+6=0`
\(\text{Vì }\)\(x^4\ge0\text{ }\forall\text{ }x\)
`-> x^4-2x^2+6 >0 AA x`
`->` Đa thức vô nghiệm.
a)\(M\left(x\right)=x^3-3x^2+5x+3-x^3+4x^2+x^4-5x+3\\ =x^4+x^2+6\)
\(N\left(x\right)=x^3-3x^2+5x+3+x^3-4x^2-x^4+5x-3\\ =-x^4+2x^3-7x^2+10x\)
b) \(M\left(1\right)=1^4+1^2+6=8\ne0\)
=> x=1 ko phai la nghiem M(x)
c) De M(x) co nghiem
\(x^4+x^2+6=0\)
vi \(x^4\ge0\forall x\\ x^2\ge0\forall x\\ \Rightarrow x^4+x^2+6\ge6\)
=> vo nghiem

 giúp mik với ạ, mik đang cần gấp><
giúp mik với ạ, mik đang cần gấp><











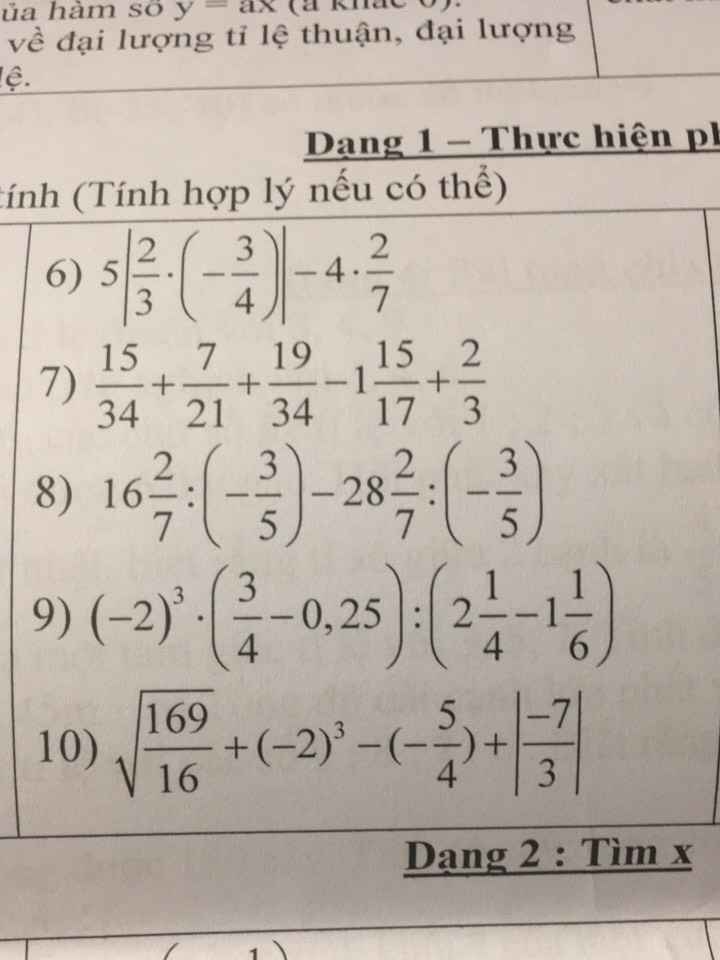
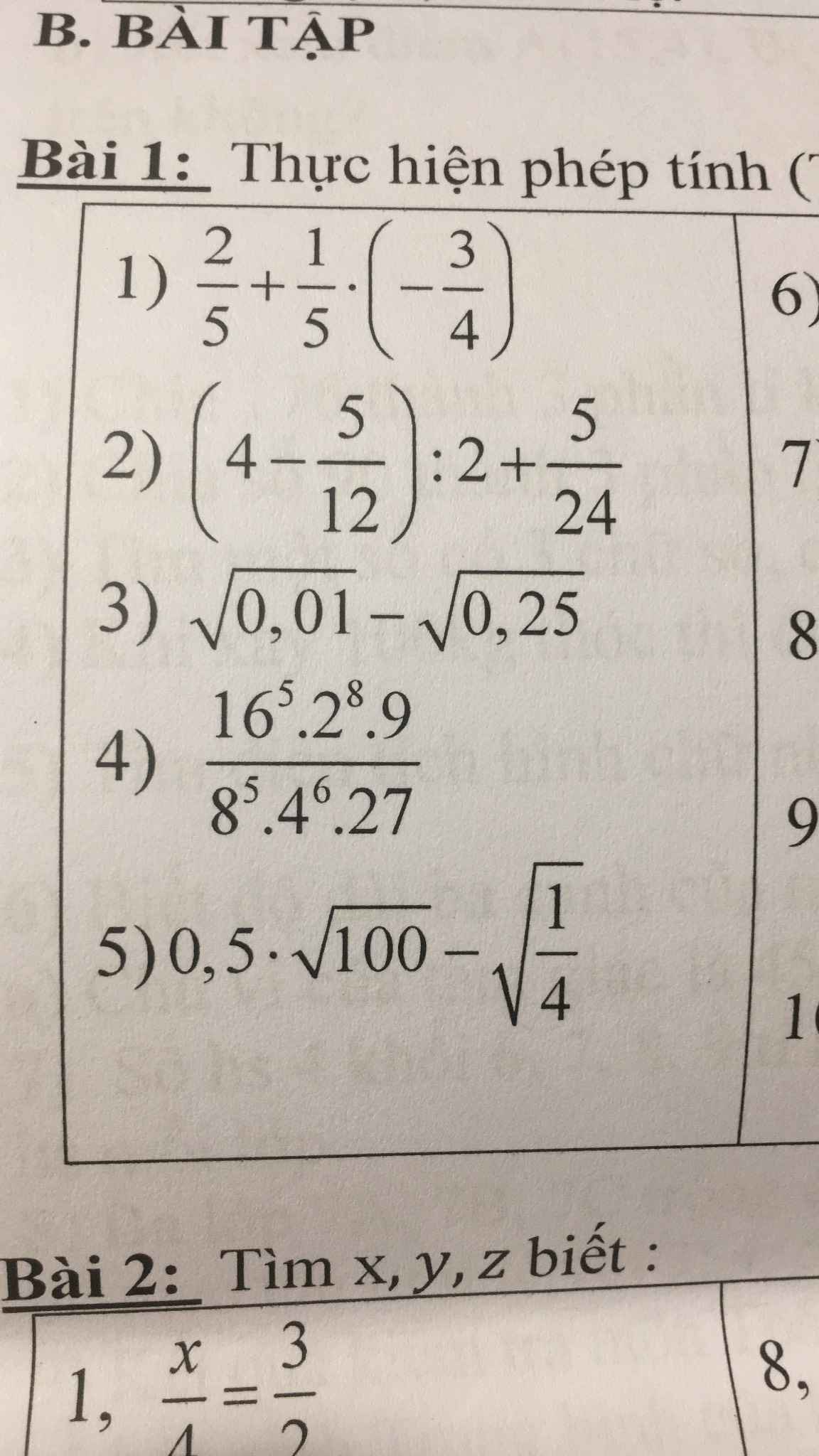

 mn giúp mik vs ạ. Mik đang cần gấp
mn giúp mik vs ạ. Mik đang cần gấp