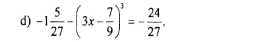a) \(A=1+2+2^2+...+2^{50}\)
\(\Rightarrow2A=2+2^2+2^3+...+2^{51}\)
\(\Rightarrow A=2A-A=2+2^2+2^3+...+2^{51}-1-2-2^2-...-2^{50}=2^{51}-1\)
\(\Rightarrow A+1=2^{51}-1+1=2^{51}=2^{n+1}\Rightarrow n=50\)
b) \(B=4+4^2+4^3+...+4^{99}\)
\(\Rightarrow4B=4^2+4^3+4^4+...+4^{100}\)
\(\Rightarrow3B=4B-B=4^2+4^3+...+4^{100}-4-4^2-...-4^{99}=4^{100}-4< 4^{100}=\left(4^2\right)^{50}=16^{50}\)

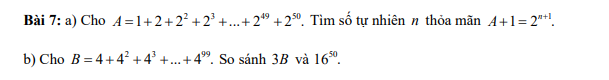










 nhanh lên nhé các bn ơi !!!
nhanh lên nhé các bn ơi !!!