a. EM tự giải
b.
\(\Delta=1-4\left(1-m\right)>0\Rightarrow m>\dfrac{3}{4}\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=1\\x_1x_2=1-m\end{matrix}\right.\)
Để biểu thức đề bài xác định \(\Rightarrow x_1x_2\ne0\Rightarrow m\ne1\)
Khi đó ta có:
\(2\left(\dfrac{1}{x_1}+\dfrac{1}{x_2}\right)+x_1x_2+3=0\)
\(\Leftrightarrow\dfrac{2\left(x_1+x_2\right)}{x_1x_2}+x_1x_2+3=0\)
\(\Leftrightarrow\dfrac{2}{1-m}+1-m+3=0\)
\(\Leftrightarrow\dfrac{2}{1-m}+4-m=0\)
\(\Rightarrow2+\left(4-m\right)\left(1-m\right)=0\)
\(\Leftrightarrow m^2-5m+6=0\Rightarrow\left[{}\begin{matrix}m=2\\m=3\end{matrix}\right.\) (thỏa mãn)


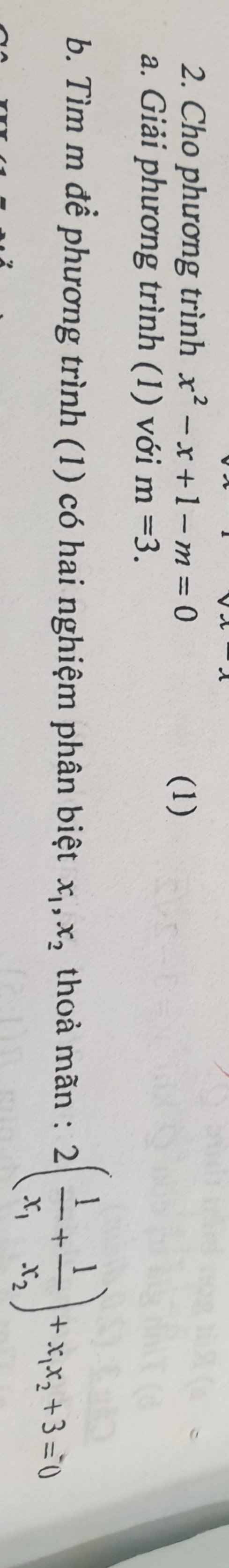






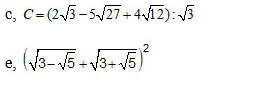
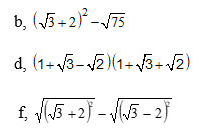 các bạn giải hộ mik mấy câu này vs mik đag cần gấp
các bạn giải hộ mik mấy câu này vs mik đag cần gấp






