a) \(\dfrac{x^2+2}{x^3-1}+\dfrac{x+1}{x^2+x+1}+\dfrac{1}{1-x}\)
\(=\dfrac{x^2+2}{\left(x-1\right)\left(x^2+x+1\right)}+\dfrac{x+1}{x^2+x+1}+\dfrac{1}{1-x}\)
\(=\dfrac{x^2+2}{\left(x-1\right)\left(x^2+x+1\right)}+\dfrac{\left(x-1\right)\left(x+1\right)}{\left(x-1\right)\left(x^2+x+1\right)}-\dfrac{x^2+x+1}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\dfrac{\left(x^2+2\right)+\left(x-1\right)\left(x+1\right)-\left(x^2+x+1\right)}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\dfrac{x^2+2+x^2-1-x^2-x-1}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\dfrac{x^2-x}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\dfrac{x\left(x-1\right)}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\dfrac{x}{x^2+x+1}\)
a)ĐKXĐ:x khác 1
C=x^2+2/(x-1)(x^2+x+1) +(x+1)(x-1)/(x-1)(x^2+x+1) - (x^2+x+1)/(x-1)(x^2+x+1)
C=x^2+2+x^2-1-x^2-x-1/(x-1)(x^2+x+1)
C=x^2-x/(x-1)(x^2+x+1)
C=x(x-1)/(x-1)(x^2+x+1)
C=x/x^2+x+1
b)Xét C-1/3=x/x^2+x+1 -x^2+x+1/x^2+x+1
=-(x^2+1)/x^2+x+1
=-(x^2+1)/(x+1/2)^2+3/4
Vì x^2+1/(x+1/2)^2+3/4 >0
=>C-1/3=-(x^2+1)/(x+1/2)^2+3/4<0
=>C<1/3












 ai giúp mik bài này đc ko ạ, mik cảm ơn!
ai giúp mik bài này đc ko ạ, mik cảm ơn!






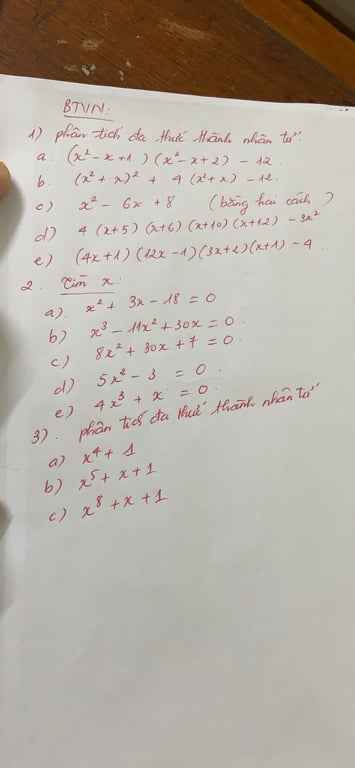

 ai giải giúp em mấy bài toán này vs ạ giải chi tiết giúp em ạ
ai giải giúp em mấy bài toán này vs ạ giải chi tiết giúp em ạ