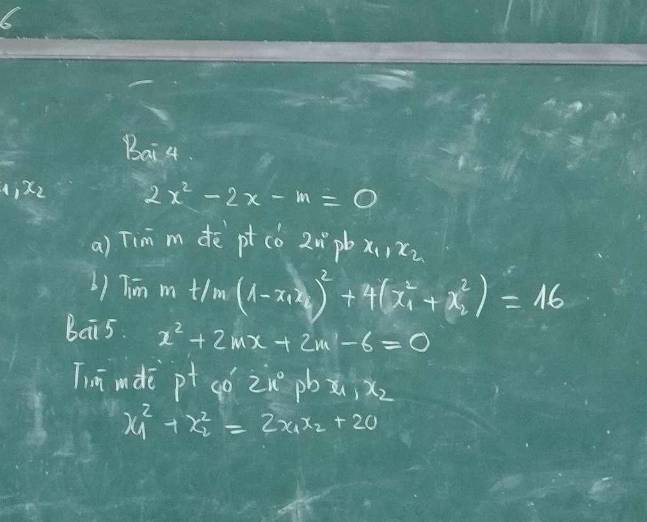b: \(\text{Δ}=\left[\left(2m+1\right)\right]^2-4\left(m^2+1\right)\)
\(=4m^2+4m+1-4m^2-4=4m-3\)
Để phương trình có hai nghiệm phân biệt thì Δ>0
=>4m-3>0
=>4m>3
=>\(m>\dfrac{3}{4}\)
Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=2m+1\\x_1x_2=\dfrac{c}{a}=m^2+1\end{matrix}\right.\)
\(\left(x_1+1\right)^2+\left(x_2+1\right)^2=13\)
=>\(x_1^2+x_2^2+2\left(x_1+x_2\right)+2=13\)
=>\(\left(x_1+x_2\right)^2-2x_1x_2+2\left(x_1+x_2\right)=11\)
=>\(\left(2m+1\right)^2-2\left(m^2+1\right)+2\left(2m+1\right)-11=0\)
=>\(4m^2+4m+1-2m^2-2+4m+2-11=0\)
=>\(2m^2+8m-10=0\)
=>\(m^2+4m-5=0\)
=>(m+5)(m-1)=0
=>\(\left[{}\begin{matrix}m=-5\left(loại\right)\\m=1\left(nhận\right)\end{matrix}\right.\)
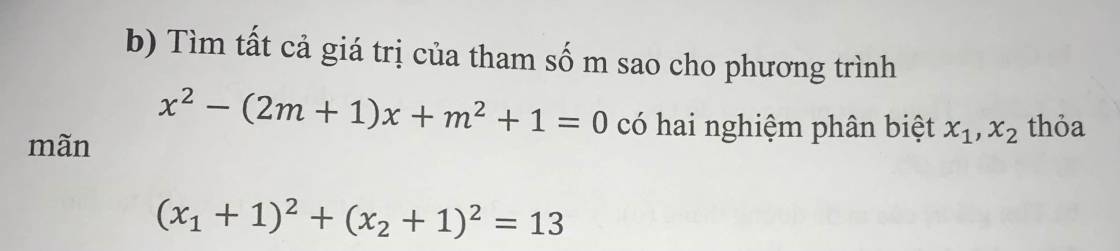
Mn giúp mik với,bh mik đang cần gấp lắm 19h30 mik phải có bài r nên mn giúp mik với 
