\(a,\dfrac{2}{1.3}+\dfrac{2}{3.5}+...+\dfrac{2}{99.101}=1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{99}-\dfrac{1}{101}=1-\dfrac{1}{101}=\dfrac{100}{101}\\ b,\dfrac{5}{1.3}+\dfrac{5}{3.5}+...+\dfrac{5}{99.101}=\dfrac{5}{2}\left(\dfrac{2}{1.3}+\dfrac{2}{3.5}+...+\dfrac{2}{99.101}\right) =\dfrac{5}{2}.\dfrac{100}{101}=\dfrac{250}{101}\)
\(c,\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{99.100}=\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{99}-\dfrac{1}{100}=\dfrac{1}{2}-\dfrac{1}{100}=\dfrac{49}{100}\\ d,\dfrac{5}{1.4}+\dfrac{5}{4.7}+...+\dfrac{5}{100.103}=\dfrac{5}{3}\left(\dfrac{3}{1.4}+\dfrac{3}{4.7}+...+\dfrac{3}{100.103}\right)=\dfrac{5}{2}.\left(1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{7}+...+\dfrac{1}{100}-\dfrac{1}{103}\right)=\dfrac{5}{2}.\left(1-\dfrac{1}{103}\right)=\dfrac{5}{2}.\dfrac{102}{103}=\dfrac{255}{103}\)

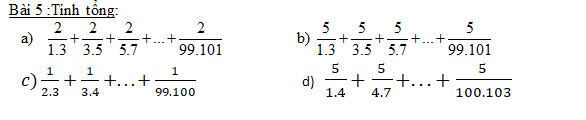





 Céc pác giúp iem bài 6 zới, iem cẻm ưn céc pác rất nhiều ;-;
Céc pác giúp iem bài 6 zới, iem cẻm ưn céc pác rất nhiều ;-; 
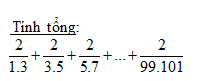



 Các pác giúp iem bài 6 zới, iem cảm ưn céc pác rất nhiều
Các pác giúp iem bài 6 zới, iem cảm ưn céc pác rất nhiều 




