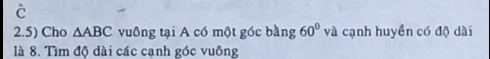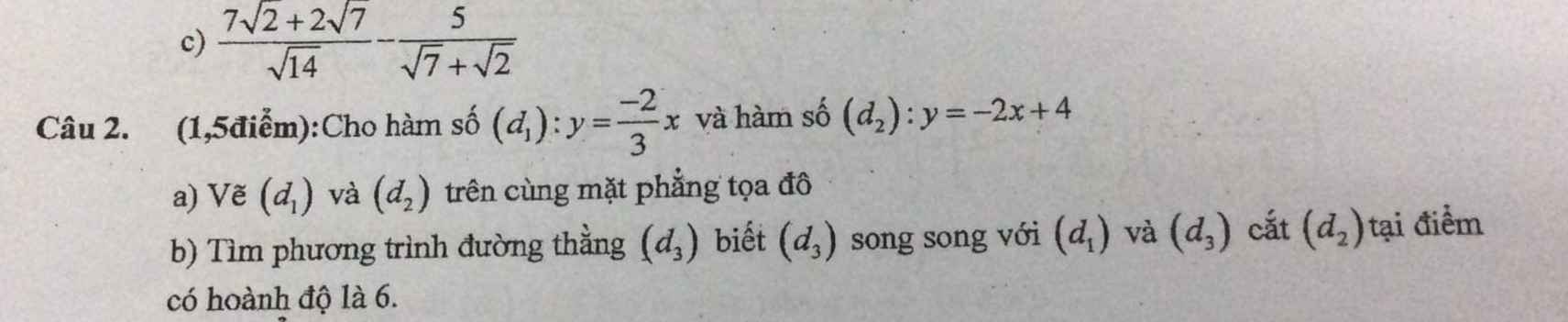a: Xét (O) có
PM là tiếp tuyến
PN là tiếp tuyến
Do đó: PM=PN
hay P nằm trên đường trung trực của MN(1)
Ta có: OM=ON
nên O nằm trên đường trung trực của MN(2)
Từ (1) và (2) suy ra OP là đường trung trực của MN
hay OP⊥MN
Xét ΔOMP vuông tại M có MK là đường cao
nên \(MP^2=PK\cdot PO\)(1)
b: Xét (O) có
ΔMIA nội tiếp
MA là đường kính
Do đó: ΔMIA vuông tại I
Xét ΔMAP vuông tại M có MI là đường cao
nên \(PI\cdot PA=MP^2\)(2)
Từ (1) và (2) suy ra \(PI\cdot PA=PK\cdot PO\)
Đúng 2
Bình luận (0)
