\(P\left(0\right)=c⋮19\)
\(P\left(1\right)=a+b+c⋮19\), mà \(c⋮19\Rightarrow a+b⋮19\) (1)
\(P\left(-2\right)=4a-2b+c⋮19\Rightarrow4a-2b⋮19\) (2)
(1);(2) \(\Rightarrow2\left(a+b\right)+4a-2b⋮19\)
\(\Rightarrow6a⋮19\)
Do 6 và 19 nguyên tố cùng nhau \(\Rightarrow a⋮19\)
Lại có \(a+b⋮19\Rightarrow b⋮19\)
\(\Rightarrow\left\{{}\begin{matrix}a⋮19\\b⋮19\\c⋮19\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a^{2017}⋮19\\b^{2018}⋮19\\c^{2019}⋮19\end{matrix}\right.\)
\(\Rightarrow A⋮2019\)





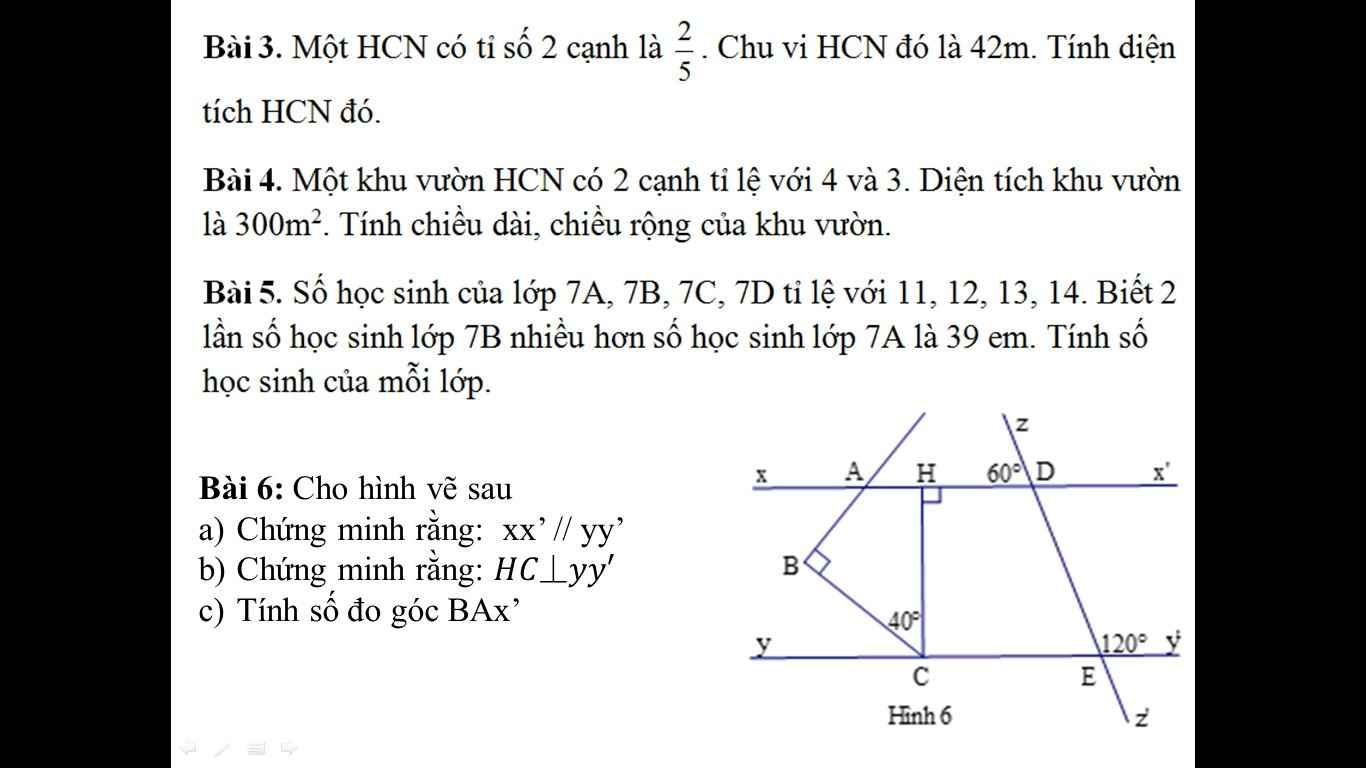


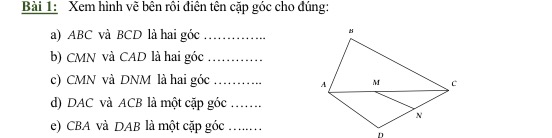


 giúp em với ạ em đang cần gấp lắm ạ em cảm ơn trước
giúp em với ạ em đang cần gấp lắm ạ em cảm ơn trước




 mn ơi! giúp em câu này với em cần gấp lắm! em cảm ơn mọi người ạ=:>
mn ơi! giúp em câu này với em cần gấp lắm! em cảm ơn mọi người ạ=:> giúp em với ạ e, đang cần gấp lắm ạ
giúp em với ạ e, đang cần gấp lắm ạ
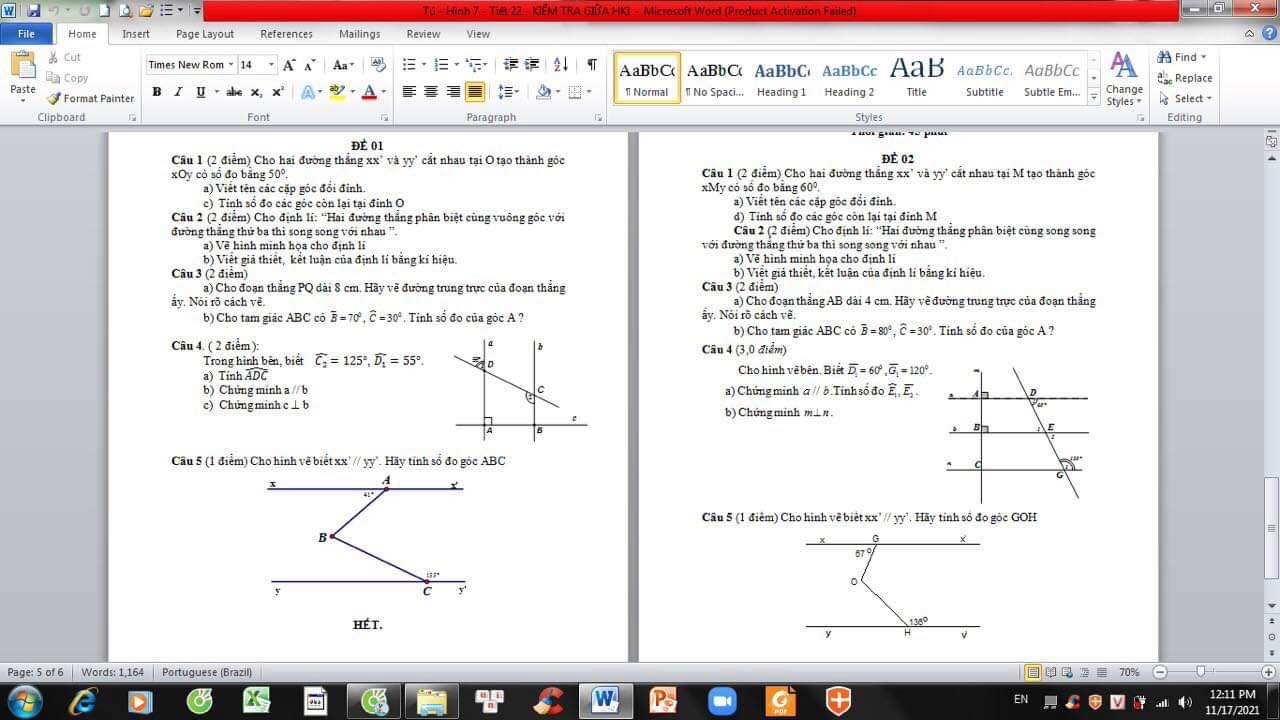

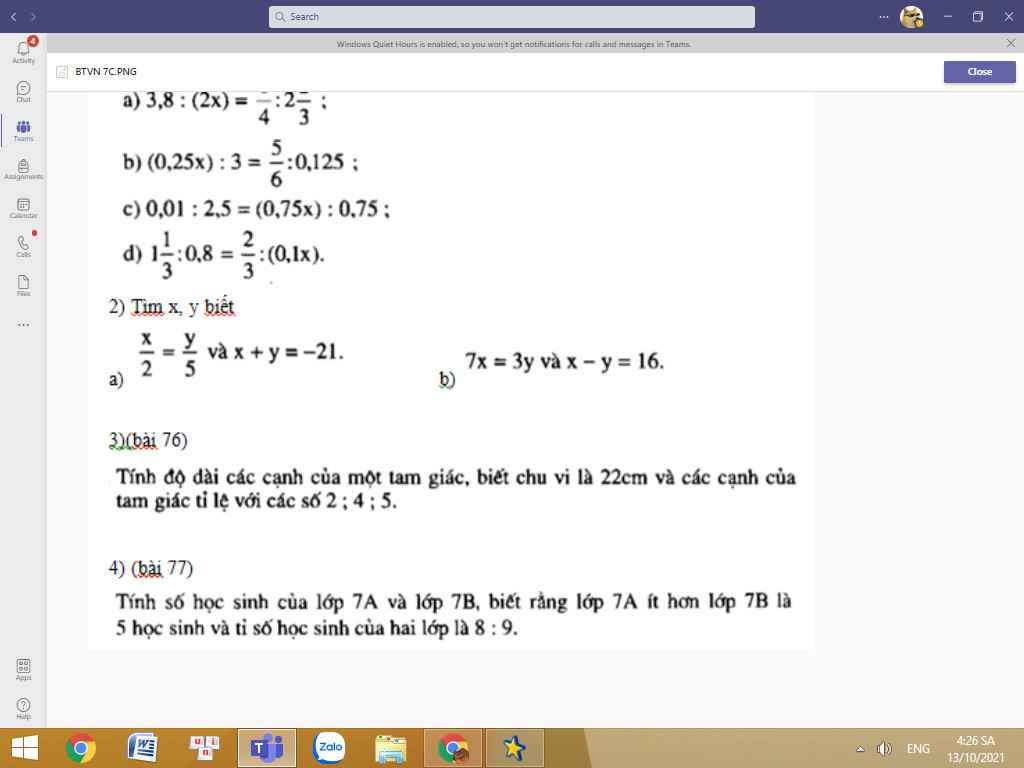 ai giúp em làm câu này vs em đang cần gấp ạ
ai giúp em làm câu này vs em đang cần gấp ạ