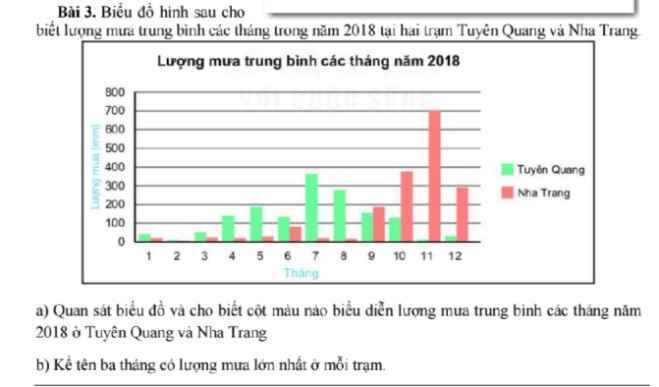
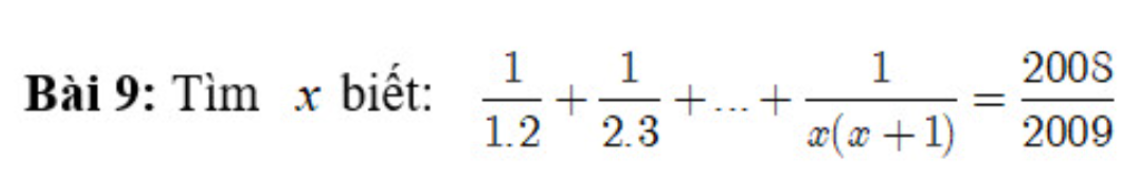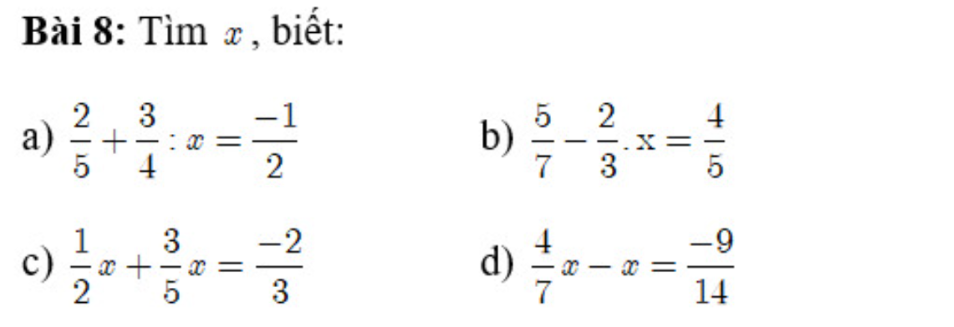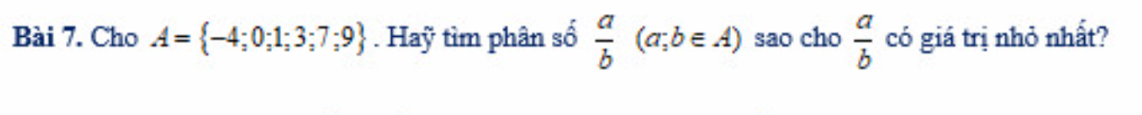\(\dfrac{1}{1\times2}+\dfrac{1}{2\times3}+...+\dfrac{1}{x\left(x+1\right)}=\dfrac{2008}{2009}\)
\(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{x}-\dfrac{1}{x+1}=\dfrac{2008}{2009}\)
\(1-\dfrac{1}{x+1}=\dfrac{2008}{2009}\)
\(\dfrac{x+1-1}{x+1}=\dfrac{2008}{2009}\)
\(\dfrac{x}{x+1}=\dfrac{2008}{2009}\)
\(\Leftrightarrow2008x+2008=2009x\)
\(\Leftrightarrow x=2008\)