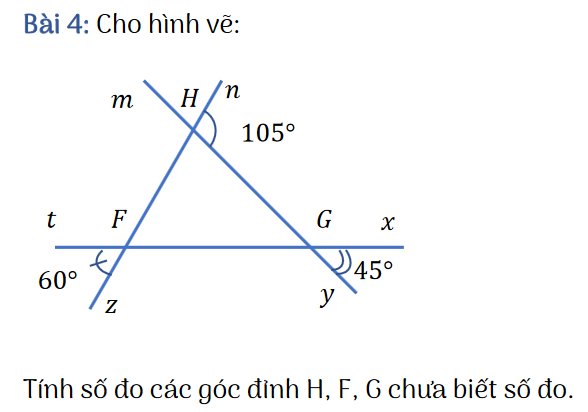
Ta có: \(\hat{mHn}+\hat{nHg}=180^0\) (hai góc kề bù)
=>\(\hat{mHn}=180^0-105^0=75^0\)
Ta có: \(\hat{mHn}=\hat{FHG}\) (hai góc đối đỉnh)
mà \(\hat{mHn}=75^0\)
nên \(\hat{FHG}=75^0\)
Ta có: \(\hat{nHG}=\hat{mHF}\) (hai góc đối đỉnh)
mà \(\hat{nHG}=105^0\)
nên \(\hat{mHF}=105^0\)
Ta có: \(\hat{tFz}+\hat{tFH}=180^0\) (hai góc kề bù)
=>\(\hat{tFH}=180^0-60^0=120^0\)
Ta có: \(\hat{tFH}=\hat{zFG}\) (hai góc đối đỉnh)
mà \(\hat{tFH}=120^0\)
nên \(\hat{zFG}=120^0\)
Ta có: \(\hat{tFz}=\hat{HFG}\) (hai góc đối đỉnh)
mà \(\hat{tFz}=60^0\)
nên \(\hat{HFG}=60^0\)
Ta có: \(\hat{xGy}+\hat{xGH}=180^0\) (hai góc kề bù)
=>\(\hat{xGH}=180^0-45^0=135^0\)
Ta có: \(\hat{xGH}=\hat{yGF}\) (hai góc đối đỉnh)
mà \(\hat{xGH}=135^0\)
nên \(\hat{yGF}=135^0\)
Ta có: \(\hat{xGy}=\hat{HGF}\) (hai góc đối đỉnh)
mà \(\hat{xGy}=45^0\)
nên \(\hat{HGF}=45^0\)