Ta có: \(x^2+\dfrac{1}{x^2}=7\)
\(\Leftrightarrow\left(x+\dfrac{1}{x}\right)^2-2=7\)
\(\Leftrightarrow\left(x+\dfrac{1}{x}\right)^2=9\)
\(\Rightarrow x+\dfrac{1}{x}=3\) (vì \(x>0\))
\(\Leftrightarrow\left(x+\dfrac{1}{x}\right)^3=27\)
\(\Leftrightarrow x^3+\dfrac{1}{x^3}+3\left(x+\dfrac{1}{x}\right)=27\)
\(\Leftrightarrow x^3+\dfrac{1}{x^3}=18\)
Mặt khác: \(x^4+\dfrac{1}{x^4}=\left(x^2+\dfrac{1}{x^2}\right)^2-2=7^2-2=47\)
Khi đó: \(\left(x^3+\dfrac{1}{x^3}\right)\left(x^4+\dfrac{1}{x^4}\right)=18.47\)
\(\Leftrightarrow x^7+\dfrac{1}{x^7}+x+\dfrac{1}{x}=846\)
\(\Leftrightarrow x^7+\dfrac{1}{x^7}+3=846\)
\(\Leftrightarrow x^7+\dfrac{1}{x^7}=843\)
hay \(A=843\)
$\text{#}Toru$

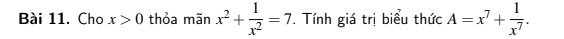






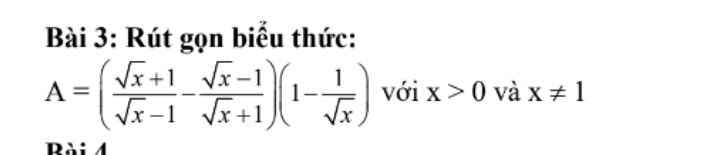








 Em cần giúp câu c và d ạ, mn giúp em với em đang cần gấp
Em cần giúp câu c và d ạ, mn giúp em với em đang cần gấp


