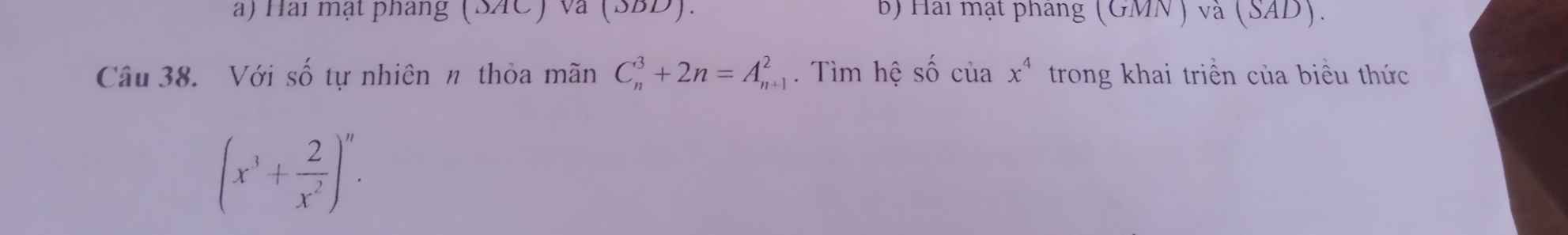Question

giúp em với

Answer 1

ĐK: \(n\ge3\)

\(C_n^3+2n=A_{n+1}^2\Leftrightarrow\dfrac{n\left(n-1\right)\left(n-2\right)}{6}+2n=\left(n+1\right)n\)

\(\Leftrightarrow\dfrac{\left(n-1\right)\left(n-2\right)}{6}+2=n+1\)

\(\Leftrightarrow n^2-9n+8=0\Rightarrow\left[{}\begin{matrix}n=1\left(loại\right)\\n=8\end{matrix}\right.\)

Xét khai triển: \(\left(x^3+2.x^{-2}\right)^8\) có SHTQ: \(C_8^k.\left(x^3\right)^k.\left(2.x^{-2}\right)^{8-k}=C_8^k.2^{8-k}.x^{5k-16}\)

Số hạng chứa \(x^4\Rightarrow5k-16=4\Rightarrow k=4\)

Hệ số: \(C_8^4.2^4=...\)