\(a,ĐK:2\le x\le4\)
Áp dụng BĐT Bunhiacopski: \(VT^2=\left(\sqrt{x-2}+\sqrt{4-x}\right)^2\le\left(1^2+1^2\right)\left(x-2+4-x\right)=4\\ \Leftrightarrow VT\le2\)
Xét vế phải \(VP=x^2-6x+11=\left(x-3\right)^2+2\ge2\)
Do đó dấu \("="\Leftrightarrow\left\{{}\begin{matrix}x-2=4-x\\x-3=0\end{matrix}\right.\Leftrightarrow x=3\left(tm\right)\)
Vậy PT có nghiệm \(x=3\)
\(b,ĐK:\dfrac{3}{2}\le x\le\dfrac{5}{2}\)
Áp dụng BĐT Bunhiacopski: \(VT^2=\left(\sqrt{2x-3}+\sqrt{5-2x}\right)^2\le\left(1^2+1^2\right)\left(2x-3+5-2x\right)=4\\ \Leftrightarrow VT\le2\)
Xét vế phải: \(3x^2-12x+14=3\left(x-2\right)^2+2\ge2\)
Dấu \("="\Leftrightarrow\left\{{}\begin{matrix}2x-3=5-2x\\x-2=0\end{matrix}\right.\Leftrightarrow x=2\left(tm\right)\)
Vậy PT có nghiệm \(x=2\)
\(c,ĐK:5\le x\le7\)
Áp dụng BĐT Bunhiacopski: \(VT^2=\left(\sqrt{7-x}+\sqrt{x-5}\right)^2\le\left(1^2+1^2\right)\left(7-x+x-5\right)=2\cdot2=4\\ \Leftrightarrow VT\le2\)
Xét vế phải: \(VP=\left(x-6\right)^2+2\ge2\)
Dấu \("="\Leftrightarrow\left\{{}\begin{matrix}7-x=x-5\\x-6=0\end{matrix}\right.\Leftrightarrow x=6\left(tm\right)\)
Vậy PT có nghiệm \(x=6\)









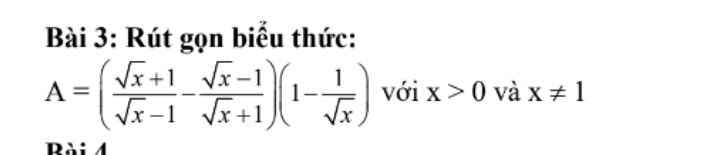








 Em cần giúp câu c và d ạ, mn giúp em với em đang cần gấp
Em cần giúp câu c và d ạ, mn giúp em với em đang cần gấp


