Bài 5:
1: Ta có: \(\widehat{BAH}+\widehat{ABC}=90^0\)(ΔHBA vuông tại H)
\(\widehat{ACB}+\widehat{ABC}=90^0\)(ΔABC vuông tại A)
Do đó: \(\widehat{BAH}=\widehat{ACB}\)
Ta có: \(\widehat{CAH}+\widehat{ACH}=90^0\)(ΔAHC vuông tại H)
\(\widehat{ABC}+\widehat{ACH}=90^0\)(ΔABC vuông tại A)
Do đó: \(\widehat{CAH}=\widehat{ABC}\)
2: \(\widehat{KAC}+\widehat{KCA}\)
\(=90^0-\widehat{KAB}+\widehat{KCA}\)
\(=90^0-\dfrac{\widehat{HAB}}{2}+\dfrac{\widehat{ACB}}{2}=90^0\)
=>ΔKAC vuông tại K
=>KA\(\perp\)KC
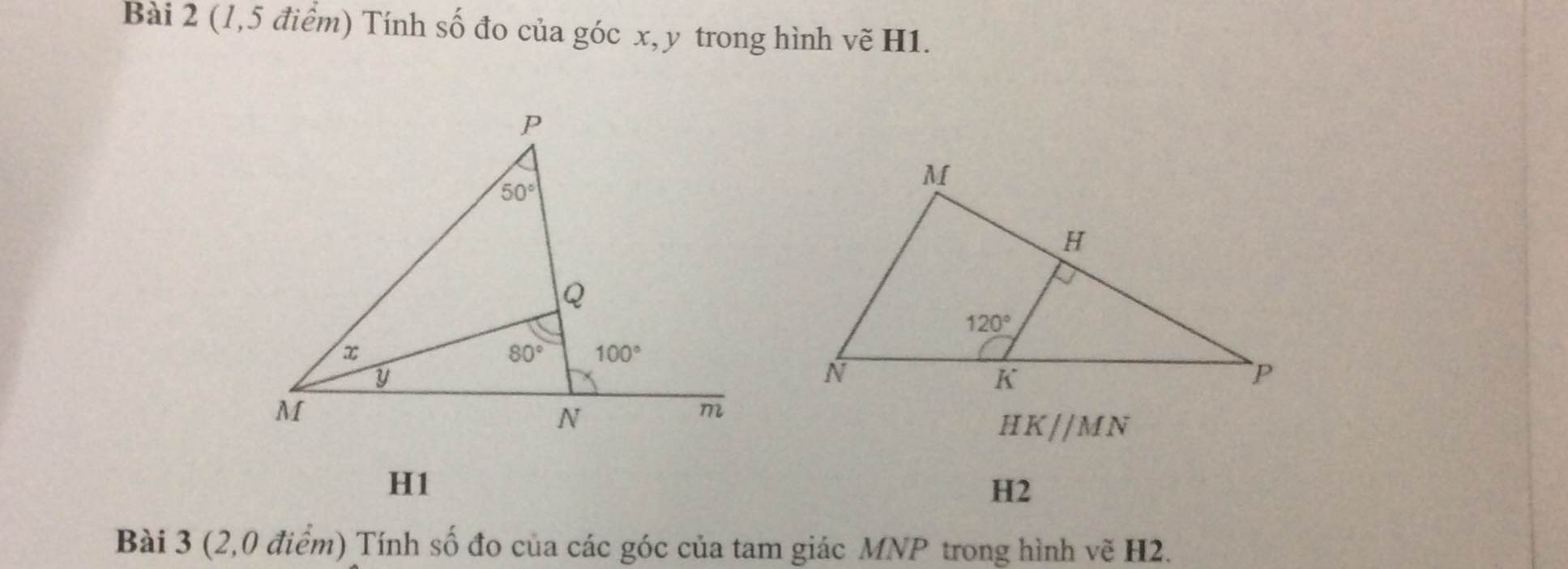
Bài 2:
Có : \(\widehat{QNm}+\widehat{QNM}=180^0\)(kề bù)
`=>`\(\widehat{QNM}=180^0-100^0=80^0\)
Xét `ΔQNM` có :
\(\widehat{M}+\widehat{Q}+\widehat{N}=180^0\)
`=>`\(y=180^0-80^0-80^0=20^0\)
Xét `ΔMPN` có :
\(\widehat{M}+\widehat{P}+\widehat{N}=180^0\)
`=>`\(M=180^0-50^0-80^0=50^0\)
Lại có : \(x+y=\widehat{M}\)
`=>`\(x=50^0-y=50^0-20^0=30^0\)
Bài 3:
Vì `HK` // `MN`
`=> `\(\widehat{H}=\widehat{M}=90^0\)(đồng vị)
\(\widehat{N}+\widehat{NKH}=180^0\)(trong cùng phía)
`=>`\(\widehat{N}=180^0-120^0=60^0\)
Xét `ΔNMP` vuông tại `M` có :
\(\widehat{N}+\widehat{P}=90^0\)(2 góc nhọn phụ nhau)
`=> `\(\widehat{P}=90^0-60^0=30^0\)

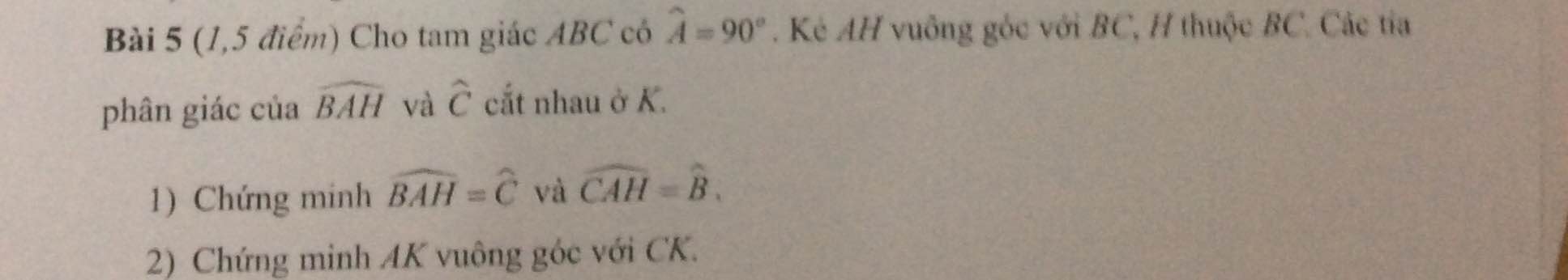















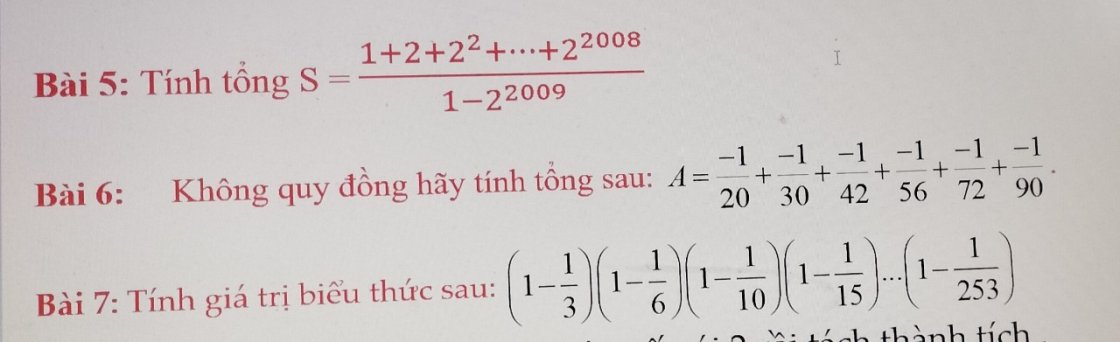 các anh chị giải giúp em bài này đc ko ạ em đang cần gấp nắm
các anh chị giải giúp em bài này đc ko ạ em đang cần gấp nắm