Bài 1:
a: ΔABC cân tại A
=>\(\widehat{ABC}=\widehat{ACB}\)
=>\(\widehat{ACB}=50^0\)
Ta có: ΔABC cân tại A
=>\(\widehat{BAC}=180^0-2\cdot\widehat{ACB}=180^0-2\cdot50^0=80^0\)
b: ΔABC cân tại A
mà AH là đường trung tuyến
nên AH là phân giác của góc BAC
Ta có: MN//BC
=>\(\widehat{AMN}=\widehat{ABC};\widehat{ANM}=\widehat{ACB}\)(Các cặp góc đồng vị)
mà \(\widehat{ABC}=\widehat{ACB}\)(ΔABC cân tại A)
nên \(\widehat{AMN}=\widehat{ANM}\)
=>ΔAMN cân tại A
Xét ΔAMH và ΔANH có
AM=AN
\(\widehat{MAH}=\widehat{NAH}\)
AH chung
Do đó: ΔAMH=ΔANH
=>HM=HN
=>ΔHMN cân tại H
Bài 2:
a: ta có: \(\widehat{ACB}+\widehat{ABC}=90^0\)(ΔABC vuông tại A)
\(\widehat{MAC}+\widehat{MAB}=\widehat{BAC}=90^0\)
mà \(\widehat{ACB}=\widehat{MAC}\left(=30^0\right)\)
nên \(\widehat{MAB}=\widehat{MBA}=90^0-30^0=60^0\)
=>ΔMAB cân tại M
=>MA=MB
Xét ΔMAC có \(\widehat{MAC}=\widehat{MCA}\left(=30^0\right)\)
nên ΔMAC cân tại M
=>MA=MC
mà MA=MB
nên MB=MC
=>M là trung điểm của BC
b: Xét ΔBAM có \(\widehat{MAB}=\widehat{MBA}=60^0\)
nên ΔBAM đều
=>BA=AM=BM
Xét ΔBKA vuông tại K và ΔMKA vuông tại K có
BA=MA
AK chung
Do đó: ΔBKA=ΔMKA
c: Xét ΔMKA vuông tại K và ΔMHC vuông tại H có
MA=MC
\(\widehat{KMA}=\widehat{HMC}\)(hai góc đối đỉnh)
Do đó: ΔMKA=ΔMHC
=>KA=HC
Bài 2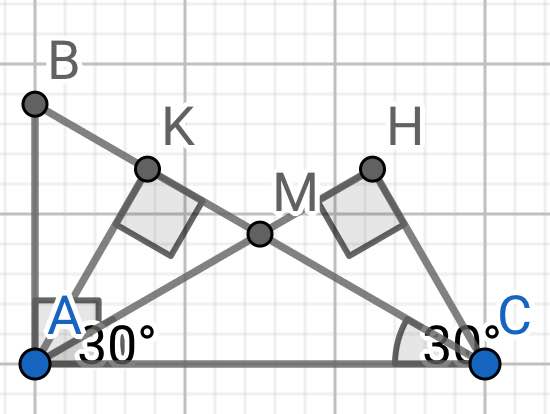
a) ABC vuông tại A (gt)
=> ∠ABC + ∠ACB = 90⁰
=> ∠ABC = 90⁰ - ∠ACB
= 90⁰ - 30⁰
= 60⁰
=> ∠ABM = 60⁰
Ta có:
∠BAM = ∠BAC - ∠CAM
= 90⁰ - 30⁰
= 60⁰
=> ∠ABM = ∠BAM = 60⁰
=> ΔΑΜΒ cân tại M
=> MA = MB (1)
ΔAMC có:
∠ACM = ∠CAM = 30⁰
=> ΔAMC cân tại M
=> MA = MC (2)
Từ (1) và (2) => MB = MC
=> M là trung điểm của BC
b) ΔΑΜΒ cân tại M (cmt)
Mà ∠BAM = 60⁰ (cmt)
=> ΔAMB đều
=> AB = AM
Xét hai tam giác vuông: ΔΒKA và ΔMKA có:
AB = AM (cmt)
AK là cạnh chung
=> ΔBKA = ΔMKA (cạnh huyền - cạnh góc vuông)
c) Xét hai tam giác vuông: ΔΑΜK và ΔCMH có:
MA = MC (cmt)
∠AMK = ∠CMH (đối đỉnh)
=> ΔΑΜK = ΔCMH (cạnh huyền - góc nhọn)
=> AK = CH (hai cạnh tương ứng)
Bài 1
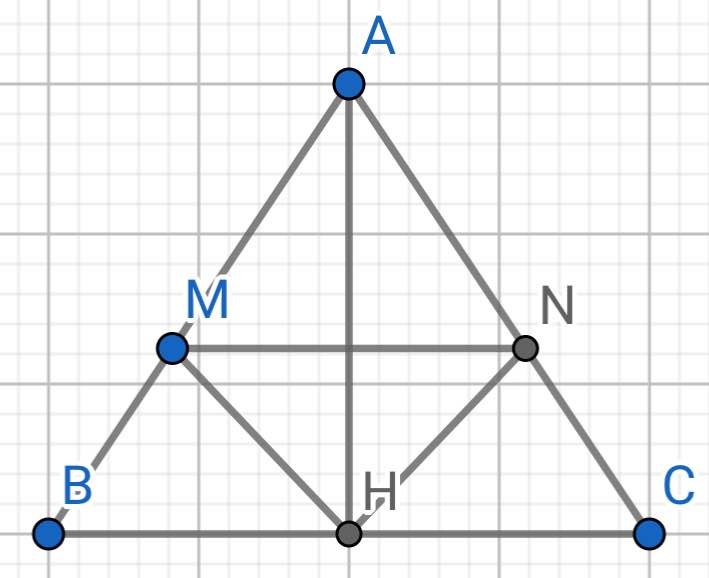
a) ΔABC cân tại A (gt)
=> ∠ABC = ∠ACB = 50⁰
Ta có:
∠ABC + ∠ACB + ∠BAC = 180⁰ (tổng ba góc trong ΔΑΒC)
=> ∠BAC = 180⁰ - (∠ABC + ∠ACB)
= 180⁰ - (50⁰ + 50⁰)
= 80⁰
b) Do MN // BC (gt)
=> ∠AMN = ∠ABC (đồng vị)
∠ANM = ∠ACB (đồng vị)
Mà ∠ABC = ∠ACB (cmt)
=> ∠AMN = ∠ANM
=> ΔAMN cân tại A
Do H là trung điểm của BC (gt)
=> BH = CH
ΔABC cân tại A (gt)
=> AB = AC
Xét ΔABH và ΔACH có:
AB = AC (cmt)
BH = CH (cmt)
AH là cạnh chung
=> ΔABH = ΔACH (c-c-c)
=> ∠BAH = ∠CAH (hai góc tương ứng)
=> ∠MAH = ∠NAH
Do ΔAMN cân tại A (cmt)
=> AM = AN
Xét AMH và ANH có:
AM = AN (cmt)
∠MAH = ∠NAH (cmt)
AH là cạnh chung
=> ΔAMH = ΔANH (c-g-c)
=> MH = NH (hai cạnh tương ứng)
=> ΔMHN cân tại H








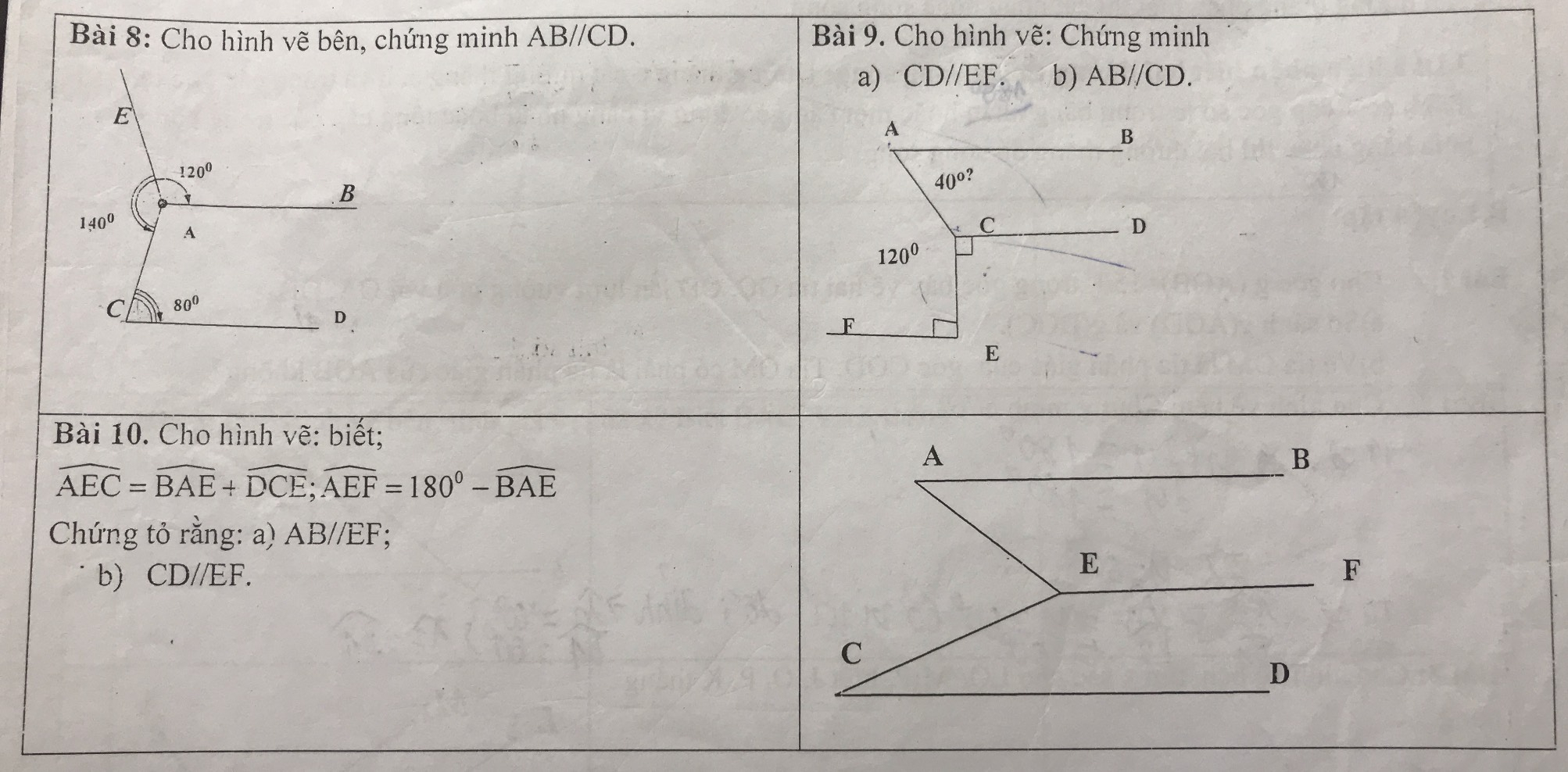 em bài 8,9,10 với ạ em gấp lắm rùi
em bài 8,9,10 với ạ em gấp lắm rùi 

 giúp em với ạ em đang cần gấp lắm ạ em cảm ơn trước
giúp em với ạ em đang cần gấp lắm ạ em cảm ơn trước
 ai giúp ewm với ạ em gấp lắm ,em cảm ơn
ai giúp ewm với ạ em gấp lắm ,em cảm ơn
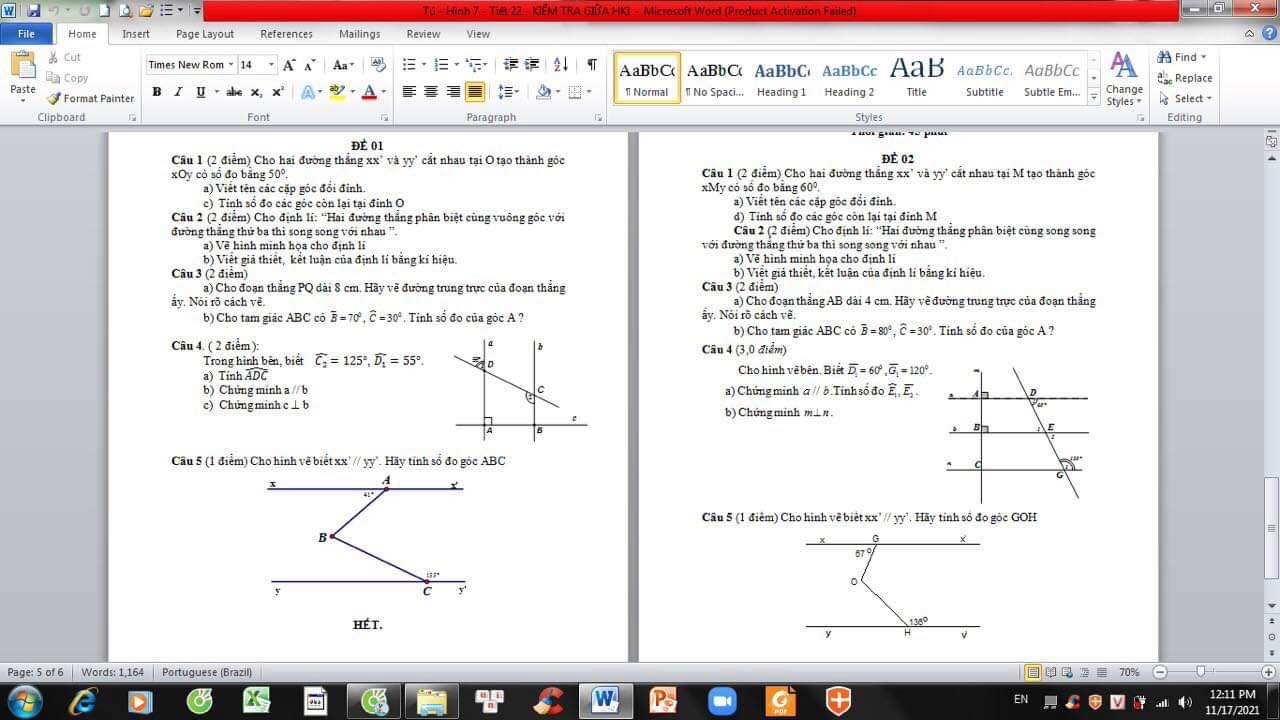

 mn ơi! giúp em câu này với em cần gấp lắm! em cảm ơn mọi người ạ=:>
mn ơi! giúp em câu này với em cần gấp lắm! em cảm ơn mọi người ạ=:>

 giúp em với ạ e, đang cần gấp lắm ạ
giúp em với ạ e, đang cần gấp lắm ạ
