Bài 1:
a: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{3}=\dfrac{y}{5}=\dfrac{z}{-2}=\dfrac{5x-y+3z}{5\cdot3-5+3\cdot\left(-2\right)}=\dfrac{124}{4}=31\)
=>\(\left\{{}\begin{matrix}x=31\cdot3=93\\y=31\cdot5=155\\z=31\cdot\left(-2\right)=-62\end{matrix}\right.\)
b: \(\dfrac{x}{4}=\dfrac{y}{6}\)
=>\(\dfrac{x}{20}=\dfrac{y}{30}\left(1\right)\)
\(\dfrac{y}{5}=\dfrac{z}{8}\)
=>\(\dfrac{y}{30}=\dfrac{z}{48}\left(2\right)\)
Từ (1),(2) suy ra \(\dfrac{x}{20}=\dfrac{y}{30}=\dfrac{z}{48}\)
mà 5x-3y-3z=-536
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{20}=\dfrac{y}{30}=\dfrac{z}{48}=\dfrac{5x-3y-3z}{5\cdot20-3\cdot30-3\cdot48}=\dfrac{-536}{-134}=4\)
=>\(\left\{{}\begin{matrix}x=4\cdot20=80\\y=4\cdot30=120\\z=4\cdot48=192\end{matrix}\right.\)
c: Đặt \(\dfrac{x}{2}=\dfrac{y}{-3}=\dfrac{z}{4}=k\)
=>x=2k; y=-3k; z=4k
\(x^2+3y^2-2z^2=-16\)
=>\(\left(2k\right)^2+3\cdot\left(-3k\right)^2-2\cdot\left(4k\right)^2=-16\)
=>\(4k^2+27k^2-32k^2=-16\)
=>\(-k^2=-16\)
=>\(k^2=16\)
=>\(\left[{}\begin{matrix}k=4\\k=-4\end{matrix}\right.\)
TH1: k=4
=>\(\left\{{}\begin{matrix}x=2\cdot4=8\\y=-3\cdot4=-12\\z=4\cdot4=16\end{matrix}\right.\)
TH2: k=-4
=>\(\left\{{}\begin{matrix}x=2k=2\cdot\left(-4\right)=-8\\y=-3k=-3\cdot\left(-4\right)=12\\z=4k=4\cdot\left(-4\right)=-16\end{matrix}\right.\)
Bài 2: Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\)
=>a=bk; c=dk
a: \(\dfrac{5a+3b}{5a-3b}=\dfrac{5\cdot bk+3b}{5bk-3b}=\dfrac{b\left(5k+3\right)}{b\left(5k-3\right)}=\dfrac{5k+3}{5k-3}\)
\(\dfrac{5c+3d}{5c-3d}=\dfrac{5\cdot dk+3d}{5dk-3d}=\dfrac{d\left(5k+3\right)}{d\left(5k-3\right)}=\dfrac{5k+3}{5k-3}\)
Do đó: \(\dfrac{5a+3b}{5a-3b}=\dfrac{5c+3d}{5c-3d}\)
b: \(\dfrac{a^4+2c^4}{b^4+2d^4}=\dfrac{\left(bk\right)^4+2\cdot\left(dk\right)^4}{b^4+2d^4}=k^4\)
\(\left(\dfrac{a^2+3c^2}{b^2+3d^2}\right)^2=\left(\dfrac{\left(bk\right)^2+3\cdot\left(dk\right)^2}{b^2+3d^2}\right)^2=\left[\dfrac{k^2\left(b^2+3d^2\right)}{b^2+3d^2}\right]^2=\left(k^2\right)^2=k^4\)
Do đó: \(\dfrac{a^4+2c^4}{b^4+2d^4}=\left(\dfrac{a^2+3c^2}{b^2+3d^2}\right)^2\)
Bài 3:
\(\dfrac{a+b}{c+d}=\dfrac{a-b}{c-d}\)
=>(a+b)(c-d)=(a-b)(c+d)
=>\(ac-ad+bc-bd=ac+ad-bc-bd\)
=>-2ad=-2bc
=>ad=bc
=>\(\dfrac{a}{b}=\dfrac{c}{d}\)

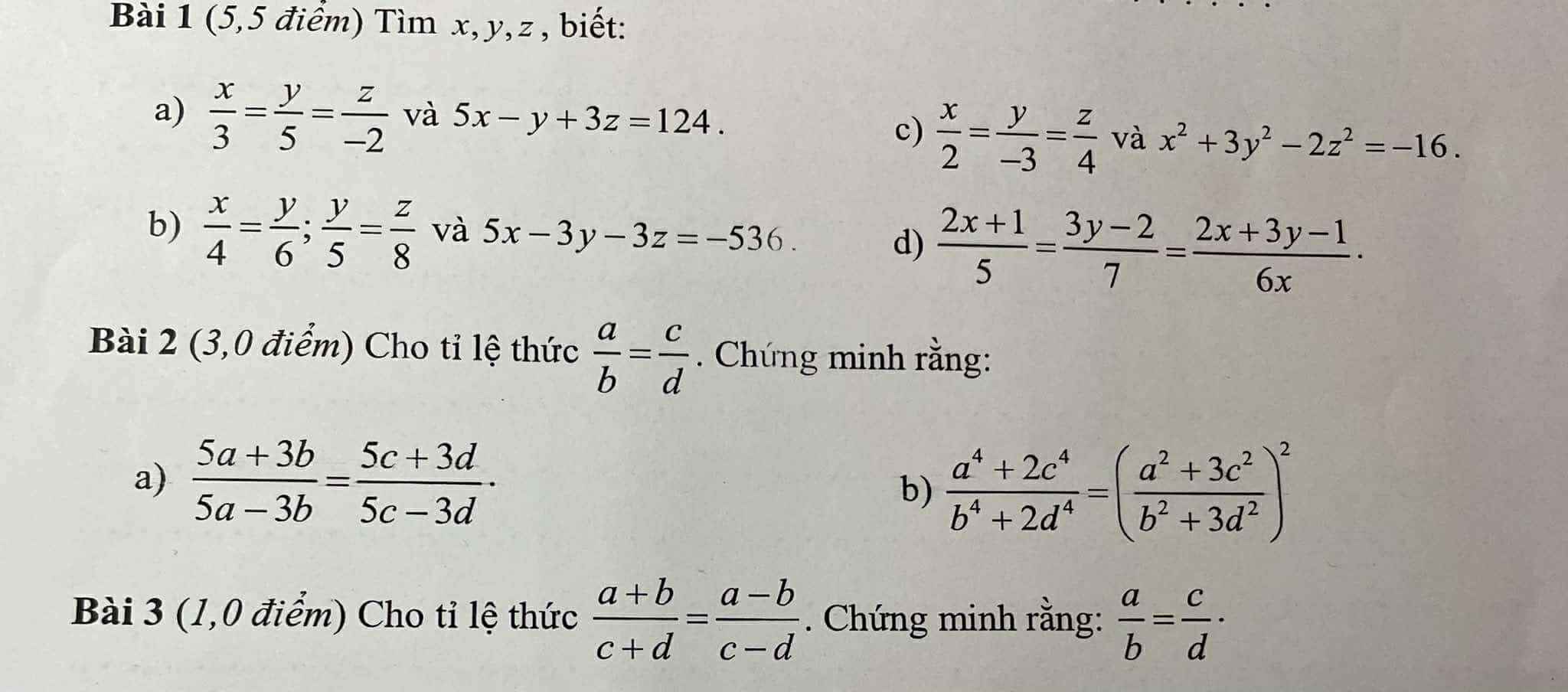




 giúp em với ạ em đang cần gấp ạ. Bài nào làm đc trc thì làm trc giúp em với ạ
giúp em với ạ em đang cần gấp ạ. Bài nào làm đc trc thì làm trc giúp em với ạ

 giúp em với ạ em cần gấp ạ
giúp em với ạ em cần gấp ạ giúp em với ạ em cần gấp ạ
giúp em với ạ em cần gấp ạ giúp em với ạ em đang cần gấp ạ
giúp em với ạ em đang cần gấp ạ giúp em với ạ em đang cần gấp ạ :(
giúp em với ạ em đang cần gấp ạ :( giúp em với ạ em đang cần gấp lắm ạ em cảm ơn trước
giúp em với ạ em đang cần gấp lắm ạ em cảm ơn trước
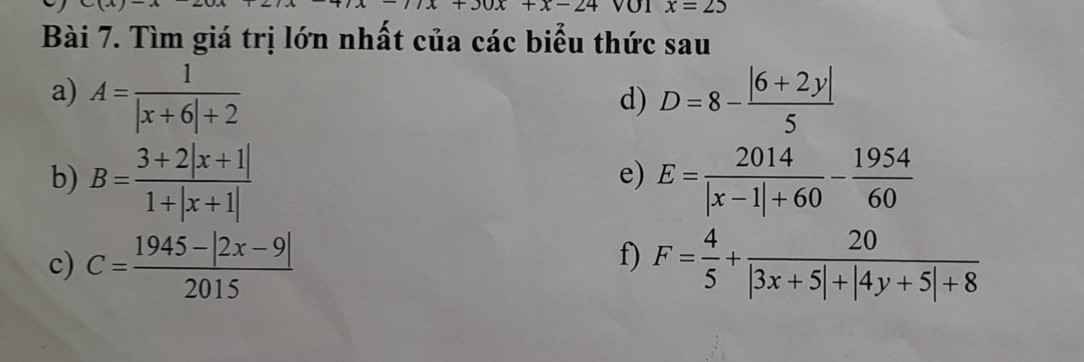
 giúp em với :( em cần gấp ạ
giúp em với :( em cần gấp ạ giúp em 3 bài này với ạ em đang cần gấp chiều em hc ròi ạ ai làm đc bài nào thì gửi luôn giúp em ạ
giúp em 3 bài này với ạ em đang cần gấp chiều em hc ròi ạ ai làm đc bài nào thì gửi luôn giúp em ạ

