Question

Giúp em với ạ em cần gấp, em cảm ơn rất nhiều

Answer 1

Bài 3:

a: Ta có: \(\widehat{BAH}+\widehat{BAC}+\widehat{KAC}=180^0\)

=>\(\widehat{BAH}+\widehat{KAC}=180^0-90^0=90^0\)

mà \(\widehat{BAH}+\widehat{HBA}=90^0\)(ΔHAB vuông tại H)

nên \(\widehat{ABH}=\widehat{CAK}\)

Xét ΔABH vuông tại H và ΔCAK vuông tại K có

AB=CA

\(\widehat{ABH}=\widehat{CAK}\)

Do đó: ΔABH=ΔCAK

=>AH=CK

b: ΔABH=ΔCAK

=>BH=AK

HK=KA+AH

mà KA=BH và AH=CK

nên HK=BH+CK

Bài 2:

a: Xét ΔEAB và ΔDAC có

AB=AC

\(\widehat{EAB}=\widehat{DAC}\)(hai góc đối đỉnh)

AE=AD

Do đó: ΔEAB=ΔDAC

=>EB=DC

b: Ta có: EC=EA+AC

DB=DA+AB

mà EA=DA và AC=AB

nên EC=DB

Xét ΔEBC và ΔDCB có

EB=DC

BC chung

EC=DB

Do đó: ΔEBC=ΔDCB

c: Xét ΔAED và ΔACB có 

\(\dfrac{AE}{AC}=\dfrac{AD}{AB}\left(AE=AD;AC=AB\right)\)

\(\widehat{EAD}=\widehat{CAB}\)(hai góc đối đỉnh)

Do đó: ΔAED~ΔACB

=>\(\widehat{AED}=\widehat{ACB}\)

mà hai góc này là hai góc ở vị trí so le trong

nên ED//BC

d: ΔABC cân tại A

mà AI là đường trung tuyến

nên AI\(\perp\)BC

mà BC//ED

nên AI\(\perp\)ED

Bài 1:

a: ΔABC vuông tại A

=>\(\widehat{ABC}+\widehat{ACB}=90^0\)

=>\(\widehat{ABC}=90^0-30^0=60^0\)

Xét ΔBAD vuông tại A và ΔBHD vuông tại H có

BD chung

\(\widehat{ABD}=\widehat{HBD}\)

Do đó: ΔBAD=ΔBHD

=>BA=BH

Xét ΔBAH có BA=BH và \(\widehat{ABH}=60^0\)

nên ΔBAH đều

b: BDlà phân giác của góc ABC

=>\(\widehat{ABD}=\widehat{HBD}=\dfrac{\widehat{ABC}}{2}=\dfrac{60^0}{2}=30^0\)

Xét ΔBHD vuông tại H và ΔBHK vuông tại H có

BH chung
HD=HK

Do đó: ΔBHD=ΔBHK

=>\(\widehat{HBD}=\widehat{HBK}=30^0\)

=>BH là phân giác của góc DBK

c: Ta có: \(\widehat{KBH}=\widehat{BCA}\left(=30^0\right)\)

mà hai góc này là hai góc ở vị trí so le tỏng

nên BK//AC

d: Ta có: ΔBAD=ΔBHD

=>DA=DH

=>D nằm trên đường trung trực của AH(1)

Ta có: BA=BH

=>B nằm trên đường trung trực của AH(2)

Từ (1),(2) suy ra BD là đường trung trực của AH

=>BD\(\perp\)AH

Answer 2

Bài 1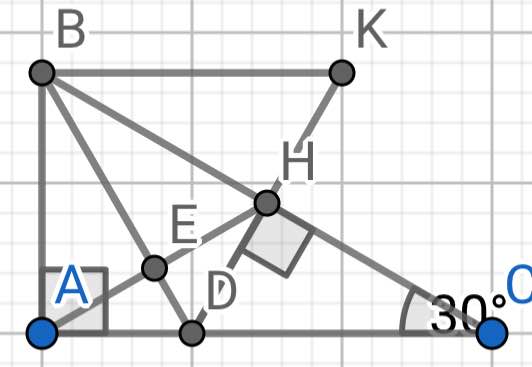
a) Do BD là tia phân giác của ∠ABC(gt)

=> ∠ABD = ∠CBD

=> ∠ABD = ∠HBD

Xét hai tam giác vuông: ΔABD và ΔHBD có:

BD là cạnh chung

∠ABD = ∠HBD (cmt)

=> ΔABD = ΔHBD (cạnh huyền - góc nhọn)

=> AB = BH (hai cạnh tương ứng)

=> ΔABH cân tại B

ΔABC vuông tại A (gt)

=> ∠ABC + ∠ACB = 90⁰

=> ∠ABC = 90⁰ - ∠ACB

= 90⁰ - 30⁰

= 60⁰

=> ∠ABH = ∠ABC = 60⁰

Mà ΔABH cân tại B (cmt)

=> ΔABH đều

b) Do H là trung điểm của DK (gt)

=> DH = KH

Xét hai tam giác vuông: ΔDBH và ΔKBH có:

DH = KH (cmt)

BH là cạnh chung

=> ΔDBH = ΔKBH (hai cạnh góc vuông)

c) Do BD là tia phân giác của ∠ABC (gt)

=> BD là tia phân giác của ∠ABH

=> ∠ABD = ∠HBD = ∠ABH : 2 = 60⁰ : 2 = 30⁰

Do ΔDBH = ΔKBH (cmt)

=> ∠HBD = ∠HBK (hai góc tương ứng)

=> ∠HBK = 30⁰

Mà ∠ACB = 30⁰ (gt)

=> ∠HBK = ∠ACB = 30⁰

Mà ∠HBK và ∠ACB là hai góc so le trong

=> BK // AC

d) Gọi E là giao điểm của BH và AD

Do BD là tia phân giác của ∠ABH (cmt)

=> BE là tia phân giác của ∠ABH

=> ∠ABE = ∠HBE

Xét ΔABE và ΔHBE có:

AB = HB (cmt)

∠ABE = ∠HBE (cmt)

BE là cạnh chung

=> ΔABE = ΔHBE (c-g-c)

=> ∠AEB = ∠HEB (hai góc tương ứng)

Mà ∠AEB + ∠HEB = 180⁰ (kề bù)

=> ∠AEB = ∠HEB = 180⁰ : 2 = 90⁰

=> AH ⊥ BE

=> AH ⊥ BD