`A=\frac{2x+1}{x-3}=\frac{2(x-3)+7}{x-3}=2+\frac{7}{x-3};(x\ne3)`
Để A lớn nhất thì `\frac{7}{x-3}` lớn nhất
`\Rightarrow x-3` nhỏ nhất
Mà x nguyên nên `x-3=1\Rightarrow x=4\text{ }(tm)`
Thay `x=4` vào A, ta được:
`A=2+\frac{7}{4-3}=2+7=9`
Vậy `A_{max}=9` tại `x=4`.

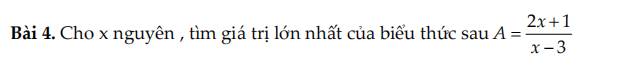 giúp em với ạ , em cảm ơn ạ
giúp em với ạ , em cảm ơn ạ 





 giúp em với ạ em cảm ơn trước ạ
giúp em với ạ em cảm ơn trước ạ


 giúp em với ạ em đang cần gấp lắm ạ em cảm ơn trước
giúp em với ạ em đang cần gấp lắm ạ em cảm ơn trước

 giúp em với ạ ai làm đc thì em xin cảm ơn ạ em đang cần gấp được ko ạ
giúp em với ạ ai làm đc thì em xin cảm ơn ạ em đang cần gấp được ko ạ
 MNG GIÚP EM BÀI 2 VỚI Ạ EM CẢM ƠN MNG NHIỀU Ạ
MNG GIÚP EM BÀI 2 VỚI Ạ EM CẢM ƠN MNG NHIỀU Ạ


 giúp em vài bài này với em đang cần gấp ạ em cảm ơn mn rất nhiều ạ
giúp em vài bài này với em đang cần gấp ạ em cảm ơn mn rất nhiều ạ