giúp em giải bài này với ạ

Bài 2. Thực hiện phép cộng các phân thức sau với điều kiện các phân thức đều xác định
a)
\[
\frac{x}{x-y} + \frac{y}{x+y} + \frac{2y^2}{x^2-y^2}
\]
\[
\frac{x^2+2}{x^2-1} + \frac{x}{x^2+x+1} + \frac{1}{1-x}
\]
b)
\[
\frac{x^3+2x}{x^3+1} + \frac{2x}{x^2-x+1} + \frac{1}{x+1}
\]
c)
d)
\[
\frac{x}{x+3} + \frac{2x}{x-3} + \frac{9-3x^2}{x^2-9}
\]
\[
\frac{2}{x-1} + \frac{2x-1}{x^2+x+1} + \frac{x^2+6x+2}{x^3-1}
\]
e)
\[
\frac{2}{x-3} + \frac{2x}{x^2-4x+3} + \frac{x}{x-1}
\]
f)
g)
\[
\frac{x}{x^2-4} + \frac{2(x^2+2x+4)}{8-x^3} + \frac{1}{x+2}
\]
h)
\[
\frac{x+2}{x-2} + \frac{1}{x} + \frac{-8}{x^2-2x}
\]
a: \(\frac{x}{x-y}+\frac{y}{x+y}+\frac{2y^2}{x^2-y^2}\)
\(=\frac{x}{x-y}+\frac{y}{x+y}+\frac{2y^2}{\left(x-y\right)\left(x+y\right)}\)
\(=\frac{x\left(x+y\right)+y\left(x-y\right)+2y^2}{\left(x-y\right)\left(x+y\right)}\)
\(=\frac{x^2+xy+xy-y^2+2y^2}{\left(x-y\right)\left(x+y\right)}=\frac{x^2+2xy+y^2}{\left(x-y\right)\left(x+y\right)}\)
\(=\frac{\left(x+y\right)^2}{\left(x-y\right)\left(x+y\right)}=\frac{x+y}{x-y}\)
b: \(\frac{x^3+2x}{x^3+1}+\frac{2x}{x^2-x+1}+\frac{1}{x+1}\)
\(=\frac{x^3+2x}{\left(x+1\right)\left(x^2-x+1\right)}+\frac{2x}{x^2-x+1}+\frac{1}{x+1}\)
\(=\frac{x^3+2x+2x\left(x+1\right)+x^2-x+1}{\left(x+1\right)\left(x^2-x+1\right)}=\frac{x^3+x^2+x+1+2x^2+2x}{\left(x+1\right)\left(x^2-x+1\right)}\)
\(=\frac{x^3+3x^2+3x+1}{\left(x+1\right)\cdot\left(x^2-x+1\right)}=\frac{\left(x+1\right)^3}{\left(x+1\right)\left(x^2-x+1\right)}=\frac{\left(x+1\right)^2}{x_{}^2-x+1}\)
c: \(\frac{x^2+2}{x^3-1}+\frac{x}{x^2+x+1}+\frac{1}{1-x}\)
\(=\frac{x^2+2}{\left(x-1\right)\left(x^2+x+1\right)}+\frac{x}{x^2+x+1}-\frac{1}{x-1}\)
\(=\frac{x^2+2+x\left(x-1\right)-x^2-x-1}{\left(x-1\right)\left(x^2+x+1\right)}=\frac{-x+1+x^2-x}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\frac{x^2-2x+1}{\left(x-1\right)\left(x^2+x+1\right)}=\frac{\left(x-1\right)^2}{\left(x-1\right)\left(x^2+x+1\right)}=\frac{x-1}{x^2+x+1}\)
d: \(\frac{x}{x+3}+\frac{2x}{x-3}+\frac{9-3x^2}{x^2-9}\)
\(=\frac{x}{x+3}+\frac{2x}{x-3}+\frac{9-3x^2}{\left(x-3\right)\left(x+3\right)}\)
\(=\frac{x\left(x-3\right)+2x\left(x+3\right)+9-3x^2}{\left(x-3\right)\left(x+3\right)}=\frac{x^2-3x+2x^2+6x+9-3x^2}{\left(x-3\right)\left(x+3\right)}=\frac{3x+9}{\left(x-3\right)\left(x+3\right)}=\frac{3}{x-3}\)
e: \(\frac{2}{x-3}+\frac{2x}{x^2-4x+3}+\frac{x}{x-1}\)
\(=\frac{2}{x-3}+\frac{2x}{\left(x-3\right)\left(x-1\right)}+\frac{x}{x-1}\)
\(=\frac{2\left(x-1\right)+2x+x-3}{\left(x-1\right)\left(x-3\right)}=\frac{2x-2+3x-3}{\left(x-1\right)\left(x-3\right)}=\frac{5x-5}{\left(x-1\right)\left(x-3\right)}=\frac{5}{x-3}\)
f: \(\frac{2}{x-1}+\frac{2x-1}{x^2+x+1}+\frac{x^2+6x+2}{x^3-1}\)
\(=\frac{2}{x-1}+\frac{2x-1}{x^2+x+1}+\frac{x^2+6x+2}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\frac{2\left(x^2+x+1\right)+\left(2x-1\right)\left(x-1\right)+x^2+6x+2}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\frac{2x^2+2x+2+2x^2-3x+1+x^2+6x+2}{\left(x-1\right)\left(x^2+x+1\right)}=\frac{5x^2+5x+5}{\left(x-1\right)\left(x^2+x+1\right)}=\frac{5}{x-1}\)
g: \(\frac{x}{x^2-4}+\frac{2\left(x^2+2x+4\right)}{8-x^3}+\frac{1}{x+2}\)
\(=\frac{x}{\left(x-2\right)\left(x+2\right)}+\frac{2\left(x^2+2x+4\right)}{\left(2-x\right)\left(x^2+2x+4\right)}+\frac{1}{x+2}\)
\(=\frac{x}{\left(x-2\right)\left(x+2\right)}+\frac{2}{2-x}+\frac{1}{x+2}\)
\(=\frac{x}{\left(x-2\right)\left(x+2\right)}-\frac{2}{x-2}+\frac{1}{x+2}\)
\(=\frac{x-2\left(x+2\right)+x-2}{\left(x-2\right)\left(x+2\right)}=\frac{2x-2-2x-4}{\left(x-2\right)\left(x+2\right)}=-\frac{6}{x^2-4}\)
h: \(\frac{x+2}{x-2}+\frac{1}{x}+\frac{-8}{x^2-2x}\)
\(=\frac{x\left(x+2\right)+x-2-8}{x\left(x-2\right)}=\frac{x^2+2x+x-10}{x\left(x-2\right)}\)
\(=\frac{x^2+3x-10}{x\left(x-2\right)}=\frac{\left(x+5\right)\left(x-2\right)}{x\left(x-2\right)}=\frac{x+5}{x}\)





 mọi người giải giúp em bài này với ạ em đang cần gấp ạ
mọi người giải giúp em bài này với ạ em đang cần gấp ạ

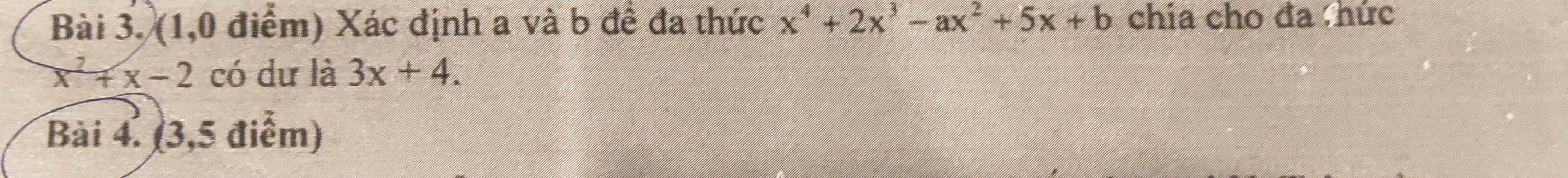 Mọi ng giúp em giải bài này với ạ, em cần gấp.
Mọi ng giúp em giải bài này với ạ, em cần gấp.


 ai giải giúp em mấy bài toán này vs ạ giải chi tiết giúp em ạ
ai giải giúp em mấy bài toán này vs ạ giải chi tiết giúp em ạ






