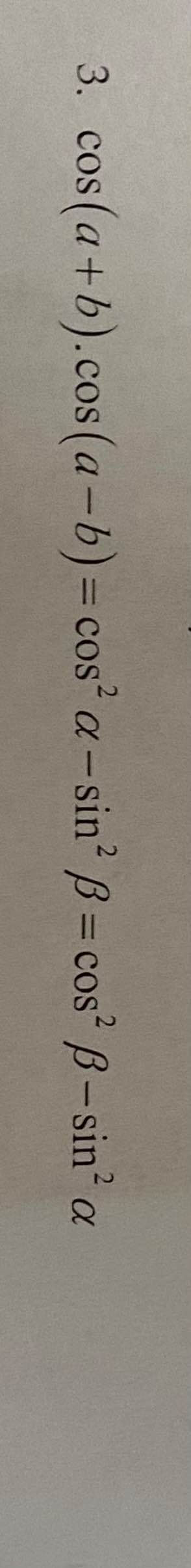\(cos\left(a+b\right)\cdot cos\left(a-b\right)\)
\(=\dfrac{1}{2}\cdot\left[cos\left(a+b+a-b\right)+cos\left(a+b-a+b\right)\right]\)
\(=\dfrac{1}{2}\left[cos\left(2a\right)+cos\left(2b\right)\right]\)
\(=\dfrac{1}{2}\left[2cos^2a-1+2cos^2b-1\right]\)
\(=cos^2a+cos^2b-1=cos^2a-sin^2b\)
\(=cos^2b+cos^2a-1=cos^2b-sin^2a\)