a) Giả sử \(2\sqrt{2}+1< 10\)
\(\Leftrightarrow2\sqrt{2}< 9\)
\(\Leftrightarrow\left(2\sqrt{2}\right)^2< 9^2\)
\(\Leftrightarrow8< 81\left(đúng\right)\)
Vậy \(2\sqrt{2}+1< 10\)
b) Giả sử \(2-\sqrt{10}>-1\)
\(\Leftrightarrow3>\sqrt{10}\)
\(\Leftrightarrow3^2>\left(\sqrt{10}\right)^2\)
\(\Leftrightarrow9>10\left(sai\right)\)
Vậy \(2-\sqrt{10}< -1\)
c) Giả sử \(5-2\sqrt{3}< 1\)
\(\Leftrightarrow4< 2\sqrt{3}\)
\(\Leftrightarrow4^2< \left(2\sqrt{3}\right)^2\)
\(\Leftrightarrow16< 12\left(sai\right)\)
Vậy \(5-2\sqrt{3}>1\)
a.
\(2\sqrt{2}+1=\sqrt{8}+1< \sqrt{9}+1=4< 10\)
Vậy \(2\sqrt{2}+1< 10\)
c.
\(5-2\sqrt{3}=5-\sqrt{12}>5-\sqrt{16}=1\)
Vậy \(5-2\sqrt{3}>1\)
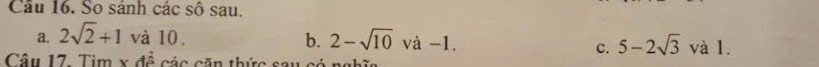
Mn giup em cau nay a!
