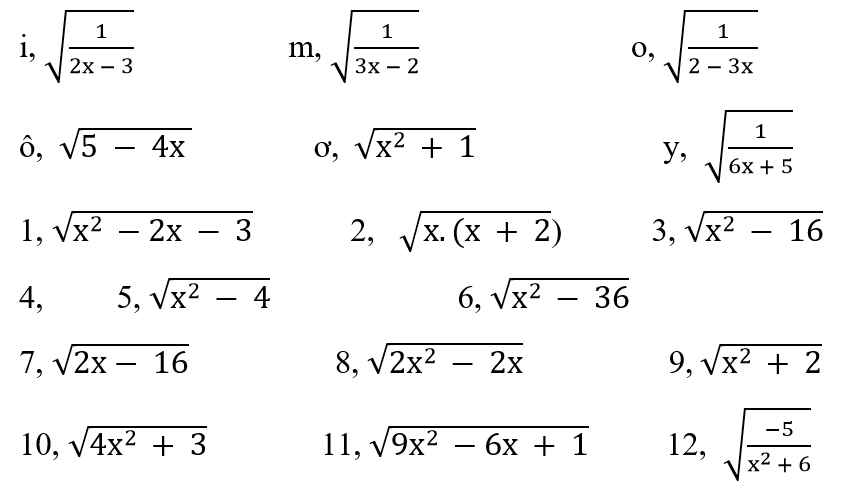Câu 2
a, Thay \(m=-2\) vào \(\left(1\right)\)
\(x^2-2x+\left(-2\right)-1=0\\ \Rightarrow x^2-2x-3=0\\ \Delta=\left(-2\right)^2-4.1.\left(-3\right)=16\\ \Leftrightarrow\left\{{}\begin{matrix}x_1=\dfrac{2+4}{2}=3\\x_2=\dfrac{2-4}{2}=-1\end{matrix}\right.\)
Vậy với m =-1 thì phương trình có hai nghiệm x =3 ; x= -1
2, \(\Delta=\left(-2\right)^2-4.1.\left(m-1\right)=4-4m+4\\ =-4m+8\)
phương trình có hai nghiệm phân biệt \(\Delta>0\\ \Rightarrow-4m+8>0\\ \Leftrightarrow m< 2\)
Áp dụng hệ thức vi ét
\(\left\{{}\begin{matrix}x_1+x_2=2\left(1\right)\\x_1.x_2=m-1\left(2\right)\end{matrix}\right.\)
Kết hợp \(\left(1\right)\) và \(x_1+2x_2=0\) ta có hệ
\(\left\{{}\begin{matrix}x_1+x_2=2\\x_1+2x_2=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x_1=4\\x_2=-2\end{matrix}\right.\)
Thay \(x_1=4;x_2=-2\) vào 2
\(\Rightarrow4.\left(-2\right)=m-1\\ \Rightarrow m=-7\left(t/m\right)\)
Vậy \(m=-7\)
Câu 1:
\(\left\{{}\begin{matrix}2x+y=5\\3x-y=5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}5x=10\\3x-y=5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{10}{5}=2\\3.2-y=5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=2\\6-y=5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=6-5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\)

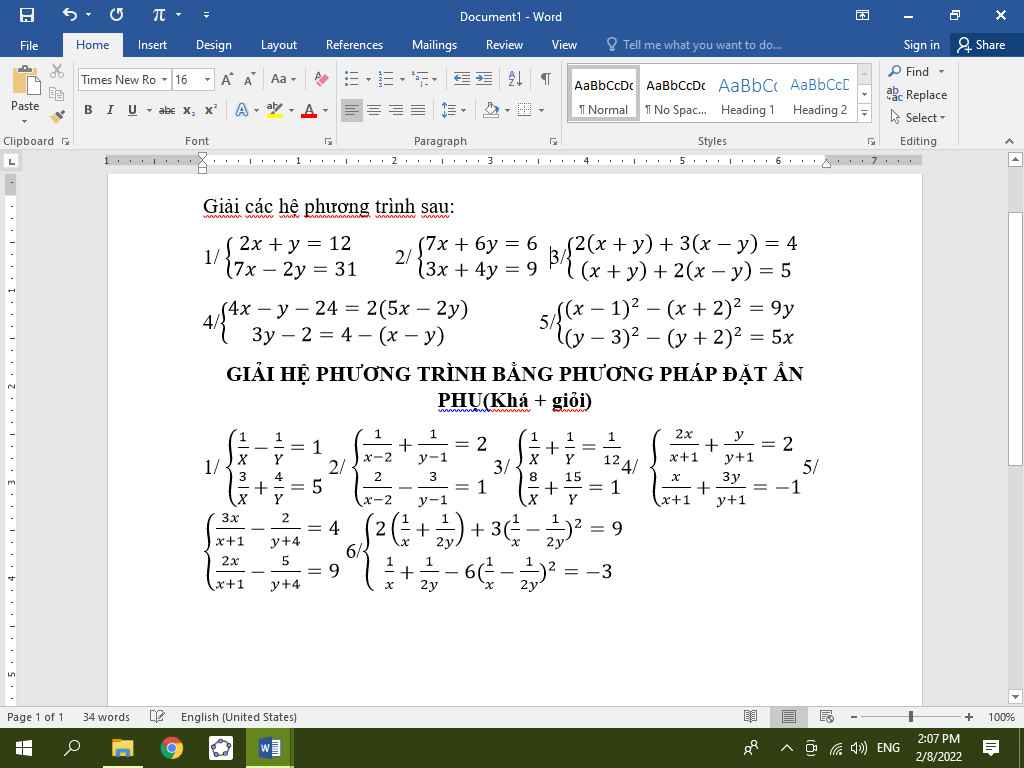
 Giúp em câu 2 với ạ. Em cảm ơn nhiều
Giúp em câu 2 với ạ. Em cảm ơn nhiều











 Giusp em với mọi người ạ. Rút gọn câu d, e, f, b giúp em với ạ, Em cảm ơn nhiều lắm.
Giusp em với mọi người ạ. Rút gọn câu d, e, f, b giúp em với ạ, Em cảm ơn nhiều lắm.