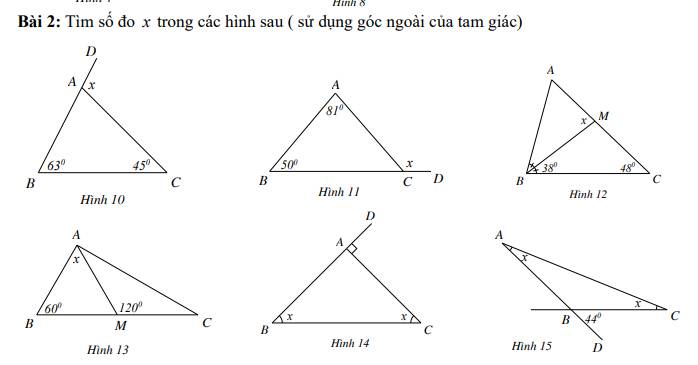
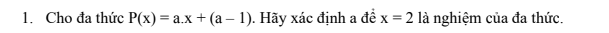Hình 10:
Xét ΔABC có \(\widehat{DAC}\) là góc ngoài tại đỉnh A
nên \(\widehat{DAC}=\widehat{ABC}+\widehat{ACB}\)
=>\(x=63^0+45^0=108^0\)
Hình 11:
Xét ΔABC có \(\widehat{ACD}\) là góc ngoài tại đỉnh C
nên \(\widehat{ACD}=\widehat{A}+\widehat{B}\)
=>\(x=81^0+50^0=131^0\)
Hình 12:
Xét ΔBMC có \(\widehat{AMB}\) là góc ngoài tại đỉnh M
nên \(\widehat{AMB}=\widehat{MBC}+\widehat{MCB}\)
=>\(x=38^0+48^0=86^0\)
Hình 13:
Xét ΔAMB có \(\widehat{AMC}\) là góc ngoài tại đỉnh M
nên \(\widehat{AMC}=\widehat{ABM}+\widehat{BAM}\)
=>\(x+60^0=120^0\)
=>\(x=60^0\)
Hình 14:
Xét ΔBAC có \(\widehat{BAC}=90^0;\widehat{ABC}=\widehat{ACB}\)
nên ΔBAC vuông cân tại A
=>x=450
Hình 15:
Xét ΔABC có \(\widehat{DBC}\) là góc ngoài tại đỉnh B
nên \(\widehat{DBC}=\widehat{BAC}+\widehat{BCA}\)
=>\(x+x=44^0\)
=>x=220






 giúp em 3 bài này với ạ em đang cần gấp chiều em hc ròi ạ ai làm đc bài nào thì gửi luôn giúp em ạ
giúp em 3 bài này với ạ em đang cần gấp chiều em hc ròi ạ ai làm đc bài nào thì gửi luôn giúp em ạ




 giúp em vài bài này với em đang cần gấp ạ em cảm ơn mn rất nhiều ạ
giúp em vài bài này với em đang cần gấp ạ em cảm ơn mn rất nhiều ạ