Bài 1:
a. Nếu số tự nhiên a chia hết cho số tự nhiên b thì a là bội của b và b là ước của a.
b.
Để tìm ước một số tự nhiên lớn hơn 1 thì ta chia số đó cho lần lượt các số tự nhiên từ 1 đến số đó, xem phép chia nào là chia hết thì số chia đó chính là ước.
$\text{Ư(27)}=\left\{1;3;9;27\right\}$
c.
Muốn tìm bội của 1 số tự nhiên khác 0 thì nhân số đó với các số 0,1,2,....
Bội của 5 nhỏ hơn 45 và lớn hơn 5 là:
$\left\{10;15;20;25;30;35;40\right\}$
Bài 2:
a/$x\in \left\{15;30\right\}$
b/ $x\in\left\{0;6;12;18;24\right\}$
c/ $x\in\left\{30;45;60;75;90\right\}$
d/ $x\in\left\{1;2;3;4;5;6;10;12;15;20\right\}$
e.
$x+16\vdots x+1$
$(x+1)+15\vdots x+1$
$15\vdots x+1$
Vậy $x+1$ là ước của $15$
$\Rightarrow x+1\in\left\{1;3;5;15\right\}$
$\Rightarrow x\in\left\{0;2;4;14\right\}$






 giúp em 3 bài này với ạ em đang cần gấp chiều em hc ròi ạ ai làm đc bài nào thì gửi luôn giúp em ạ
giúp em 3 bài này với ạ em đang cần gấp chiều em hc ròi ạ ai làm đc bài nào thì gửi luôn giúp em ạ




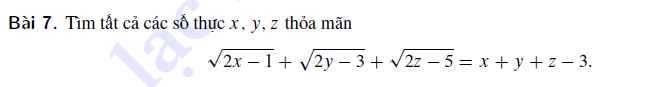

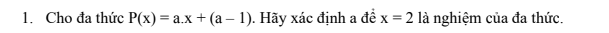



 giúp em vài bài này với em đang cần gấp ạ em cảm ơn mn rất nhiều ạ
giúp em vài bài này với em đang cần gấp ạ em cảm ơn mn rất nhiều ạ
