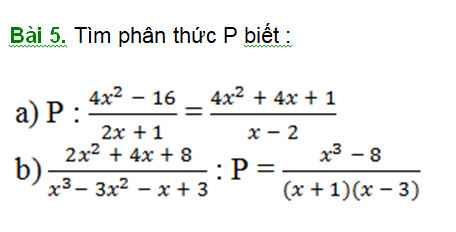\(x^4-x^3-2x-4\)
\(=x^4-2x^3+x^3-2x^2+2x^2-4x+2x-4\)
\(=\left(x-2\right)\left(x^3+x^2+2x+2\right)\)
\(=\left(x-2\right)\left(x+1\right)\left(x^2+2\right)\)
\(P\left(x\right)=\left(x^2+dx+2\right)\left(x^2+cx-2\right)\\ P\left(x\right)=x^4+cx^3-2x^2+dx^3+cdx^2-2dx+2x^2+2cx-4\\ P\left(x\right)=x^4+x^3\left(c+d\right)+cdx^2-2x\left(d-c\right)-4=x^4-x^3-2x-4\\ \Leftrightarrow\left\{{}\begin{matrix}c+d=-1\\cd=0\\d-c=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}c=-1\\d=0\end{matrix}\right.\\ \Leftrightarrow P\left(x\right)=\left(x^2+2\right)\left(x^2-x-2\right)=\left(x^2+2\right)\left(x+1\right)\left(x-2\right)\)

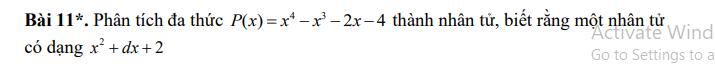






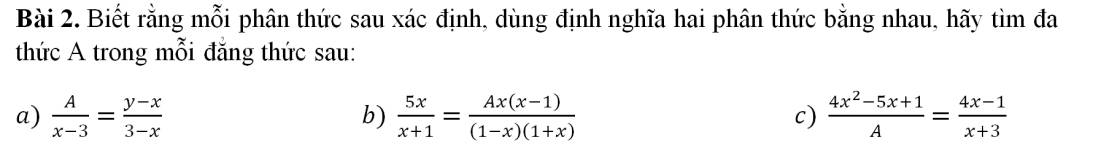 giúp em bài này với ạ ! Em cảm ơn ạ
giúp em bài này với ạ ! Em cảm ơn ạ 
 ai giải giúp em mấy bài toán này vs ạ giải chi tiết giúp em ạ
ai giải giúp em mấy bài toán này vs ạ giải chi tiết giúp em ạ
 giúp em bài này vs ạ em cảm ơn trc ạ
giúp em bài này vs ạ em cảm ơn trc ạ
 mọi người giải giúp em bài này với ạ em đang cần gấp ạ
mọi người giải giúp em bài này với ạ em đang cần gấp ạ