3.
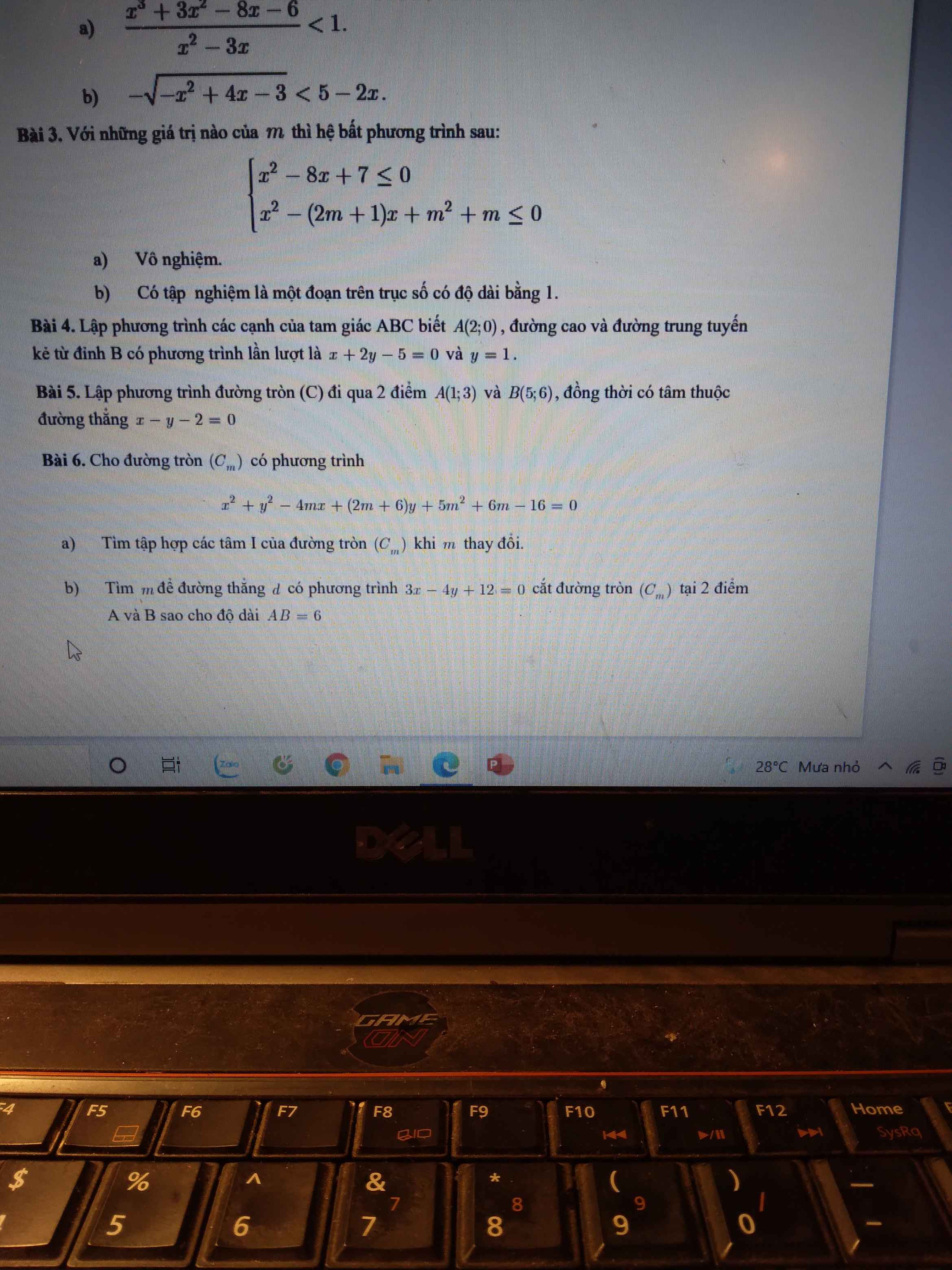
Xét \(x^2-8x+7\le0\Leftrightarrow\left(x-1\right)\left(x-7\right)\le0\Rightarrow1\le x\le7\)
Có tập nghiệm \(D_1=\left[1;7\right]\)
Xét \(x^2-\left(2m+1\right)x+m^2+m\le0\Leftrightarrow\left(x-m\right)\left(x-m-1\right)\le0\)
\(\Leftrightarrow m\le x\le m+1\) có tập nghiệm là \(D_2=\left[m;m+1\right]\)
a. Hệ BPT vô nghiệm khi \(D_1\cap D_2=\varnothing\)
\(\Leftrightarrow\left[{}\begin{matrix}m>7\\m+1< 1\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}m>7\\m< 0\end{matrix}\right.\)
b. Do \(D_2\) là đoạn có độ dài bằng \(m+1-m=1\) nên hệ có tập nghiệm là 1 đoạn dài 1 trên trục số khi: \(D_2\subset D_1\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ge1\\m+1\le7\end{matrix}\right.\) \(\Rightarrow1\le m\le6\)