3.
TH1: chữ số hàng đơn vị là 0
\(\Rightarrow5\) chữ số đầu có \(A_8^5\) cách chọn và hoán vị
TH2: chữ số hàng đơn vị khác 0 \(\Rightarrow\) có 2 cách chọn (4 và 8)
5 chữ số đầu có: \(A_8^5-A_7^4\) cách chọn và hoán vị
Tổng cộng: \(A_8^5+2\left(A_8^5-A_7^4\right)=...\) số
4.
Trước hết tìm quy luật phần vế trái, dạng \(\dfrac{C_n^k}{\left(k+1\right)\left(k+2\right)}\)
Ta có:
\(\dfrac{C_n^k}{\left(k+1\right)\left(k+2\right)}=\dfrac{n!}{k!\left(n-k\right)!\left(k+1\right)\left(k+2\right)}=\dfrac{n!\left(n+1\right)\left(n+2\right)}{k!\left(k+1\right)\left(k+2\right)\left(n-k\right)!\left(n+1\right)\left(n+2\right)}\)
\(=\dfrac{\left(n+2\right)!}{\left(k+2\right)!\left(n-k\right)!\left(n+1\right)\left(n+2\right)}=\dfrac{C_{n+2}^{k+2}}{\left(n+1\right)\left(n+2\right)}\)
Vì vậy:
\(\sum\limits^n_{k=0}\dfrac{C_n^k}{\left(k+1\right)\left(k+2\right)}=\sum\limits^n_{k=0}\dfrac{C_{n+2}^{k+2}}{\left(n+1\right)\left(n+2\right)}\)
\(\Rightarrow\dfrac{2^{100}-n-3}{\left(n+1\right)\left(n+2\right)}=\dfrac{\sum\limits^n_{k=0}C_{n+2}^{k+2}}{\left(n+1\right)\left(n+2\right)}\)
\(\Rightarrow2^{100}-n-3=\sum\limits^n_{k=0}C_{n+2}^{k+2}=C_{n+2}^2+C_{n+2}^3+...+C_{n+2}^{n+2}\) (1)
Xét khai triển:
\(\left(1+x\right)^{n+2}=\sum\limits^{n+2}_{k=0}C_{n+2}^kx^k\)
Thay \(x=1\Rightarrow2^{n+2}=\sum\limits^{k+2}_{k=0}C_{n+2}^k=C_{n+2}^0+C_{n+2}^1+C_{n+2}^2+...+C_{n+2}^{n+2}\)
\(\Rightarrow C_{n+2}^2+C_{n+2}^3+...+C_{n+2}^{n+2}=2^{n+2}-C_{n+2}^0-C_{n+2}^1=2^{n+2}-n-3\) (2)
(1);(2) \(\Rightarrow2^{100}-n-3=2^{n+2}-n-3\)
\(\Rightarrow n+2=100\Rightarrow n=98\)












 Giúp em với ạ. Cần rất gấp ạ. Em cảm ơn ạ
Giúp em với ạ. Cần rất gấp ạ. Em cảm ơn ạ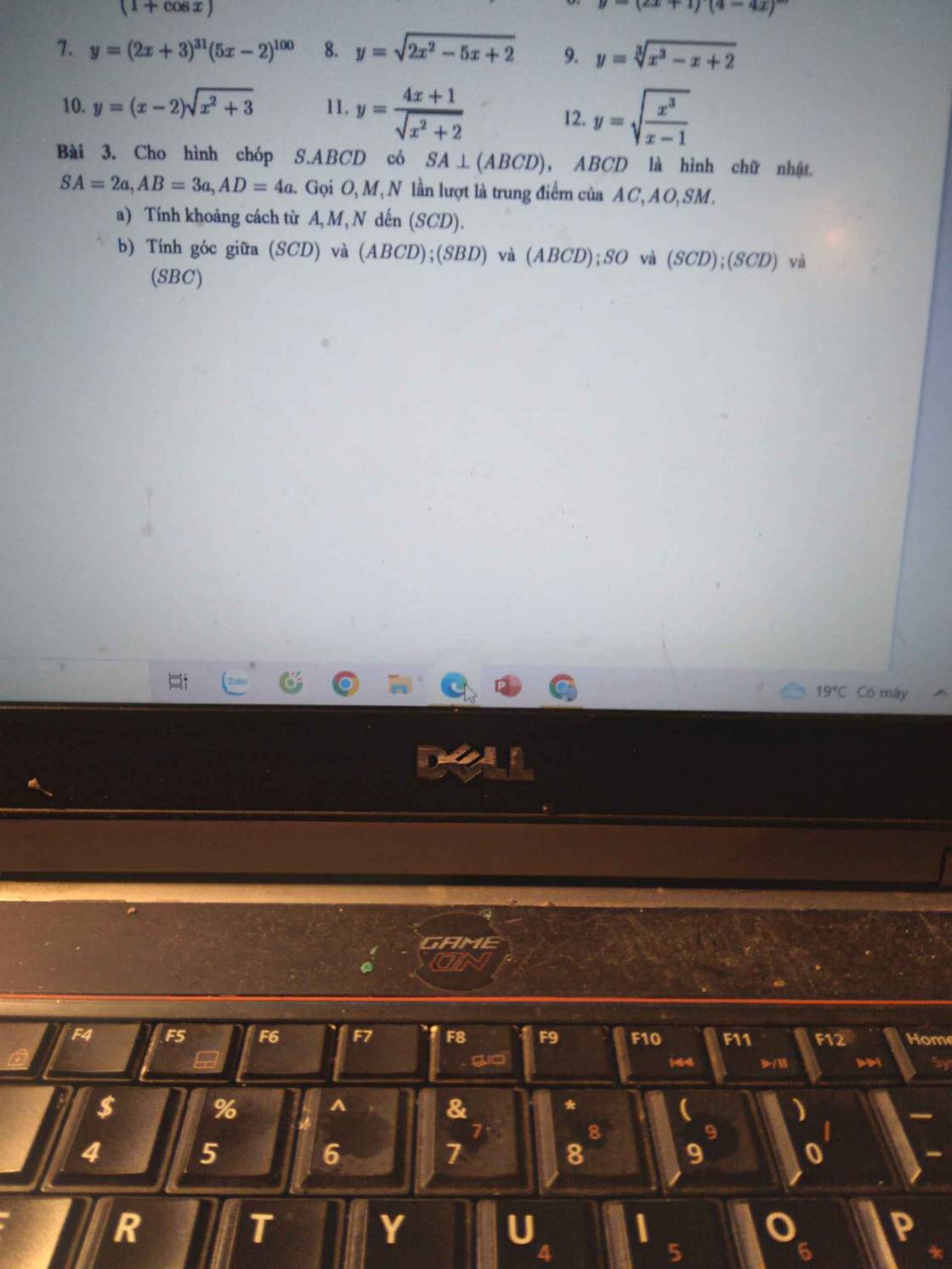 Giúp em bài 3 với ạ. Em cảm ơn ạ
Giúp em bài 3 với ạ. Em cảm ơn ạ










