9: Xét ΔBHC có HD là đường cao
nên \(S_{BHC}=\frac12\cdot HD\cdot BC\left(1\right)\)
Xét ΔABC có AD là đường cao
nên \(S_{ABC}=\frac12\cdot AD\cdot BC\left(2\right)\)
Từ (1),(2) suy ra \(\frac{S_{HBC}}{S_{ABC}}=\frac{\frac12\cdot HD\cdot BC}{\frac12\cdot AD\cdot BC}=\frac{HD}{AD}\)
Xét ΔHAC có HE là đường cao
nên \(S_{AHC}=\frac12\cdot HE\cdot AC\left(3\right)\)
Xét ΔABC có BE là đường cao
nên \(S_{ABC}=\frac12\cdot BE\cdot AC\left(4\right)\)
Từ (3),(4) suy ra \(\frac{S_{HAC}}{S_{BAC}}=\frac{HE}{BE}\)
Xét ΔHAB có HF là đường cao
nên \(S_{HAB}=\frac12\cdot HF\cdot AB\left(5\right)\)
Xét ΔABC có CF là đường cao
nên \(S_{ABC}=\frac12\cdot CF\cdot AB\left(6\right)\)
Từ (5),(6) suy ra \(\frac{S_{HAB}}{S_{ABC}}=\frac{HF}{CF}\)
\(\frac{HD}{AD}+\frac{HE}{BE}+\frac{HF}{CF}\)
\(=\frac{S_{HAB}+S_{HCA}+S_{HBC}}{S_{BAC}}=\frac{S_{BAC}}{S_{BAC}}=1\)
10: Xét ΔBEA vuông tại E có \(cosBAC=\frac{AE}{AB}\)
Xét ΔAFC vuông tại F có \(cosBAC=cosFAC=\frac{AF}{AC}\)
Do đó: \(cosBAC=\sqrt{cosBAE\cdot cosCAF}=\sqrt{\frac{AE}{AB}\cdot\frac{AF}{AC}}=\sqrt{\frac{AF}{AB}\cdot\frac{AE}{AC}}\le\frac12\left(\frac{AF}{AB}+\frac{AE}{AC}\right)\)
Xét ΔBFC vuông tại F có \(cosABC=\frac{BF}{BC}\)
Xét ΔBDA vuông tại D có \(cosABC=cosABD=\frac{BD}{BA}\)
Do đó: \(cosABC=\sqrt{cosABD\cdot cosCBF}=\sqrt{\frac{BF}{BC}\cdot\frac{BD}{BA}}=\sqrt{\frac{BD}{BC}\cdot\frac{BF}{BA}}\le\frac12\left(\frac{BD}{BC}+\frac{BF}{BA}\right)\)
Xét ΔCEB vuông tại E có \(cosACB=cosECB=\frac{CE}{CB}\)
Xét ΔCDA vuông tại D có \(cosACB=cosACD=\frac{CD}{AC}\)
Do đó: \(cosACB=\sqrt{cosACD\cdot cosBCE}=\sqrt{\frac{CE}{CB}\cdot\frac{CD}{CA}}=\sqrt{\frac{CE}{CA}\cdot\frac{CD}{CB}}\le\frac12\left(\frac{CE}{CA}+\frac{CD}{CB}\right)\)
\(cosBAC+cosABC+cosACB\le\frac12\left(\frac{AF}{AB}+\frac{BF}{AB}+\frac{AE}{AC}+\frac{CE}{AC}+\frac{BD}{BC}+\frac{CD}{BC}\right)\)
=>\(cosABC+cosACB+cosBAC\le\frac12\cdot3=\frac32\)
10: Xét ΔABC có \(\hat{ABC}+\hat{ACB}+\hat{BAC}=180^0\)
=>\(\hat{BAC}=180^0-45^0-60^0=75^0\)
Xét ΔABC có \(\frac{BC}{\sin BAC}=\frac{AC}{\sin ABC}=\frac{AB}{\sin ACB}\)
=>\(\frac{2a}{\sin75}=\frac{AB}{\sin45}=\frac{AC}{\sin60}\)
=>\(AB=2a\cdot\frac{\sin45}{\sin75}=2a\left(-1+\sqrt3\right)\) ; \(AC=2a\cdot\frac{\sin60}{\sin75}=\frac{-\sqrt6+3\sqrt2}{2}\cdot2a=\left(-\sqrt6+3\sqrt2\right)\cdot a\)
Diện tích tam giác ABC là:
\(S_{ABC}=\frac12\cdot AB\cdot AC\cdot\sin BAC\)
\(=\frac12\cdot2a\left(-1+\sqrt3\right)\cdot\left(-\sqrt6+3\sqrt2\right)\cdot a\cdot\sin75\)
\(=a\left(-1+\sqrt3\right)\left(-\sqrt6+3\sqrt2\right)\cdot a\cdot\frac{\sqrt6+\sqrt2}{4}=\left(3-\sqrt3\right)\cdot a^2\)





 giúp em câu cuối ạ
giúp em câu cuối ạ
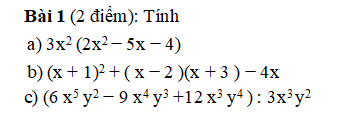

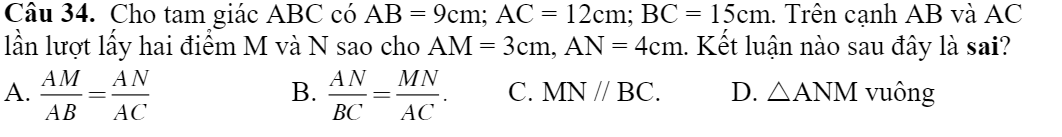








 Mn giúp em bài 3 câu bc với em tính số xấu quá, mong mn giúp ạ:(
Mn giúp em bài 3 câu bc với em tính số xấu quá, mong mn giúp ạ:(