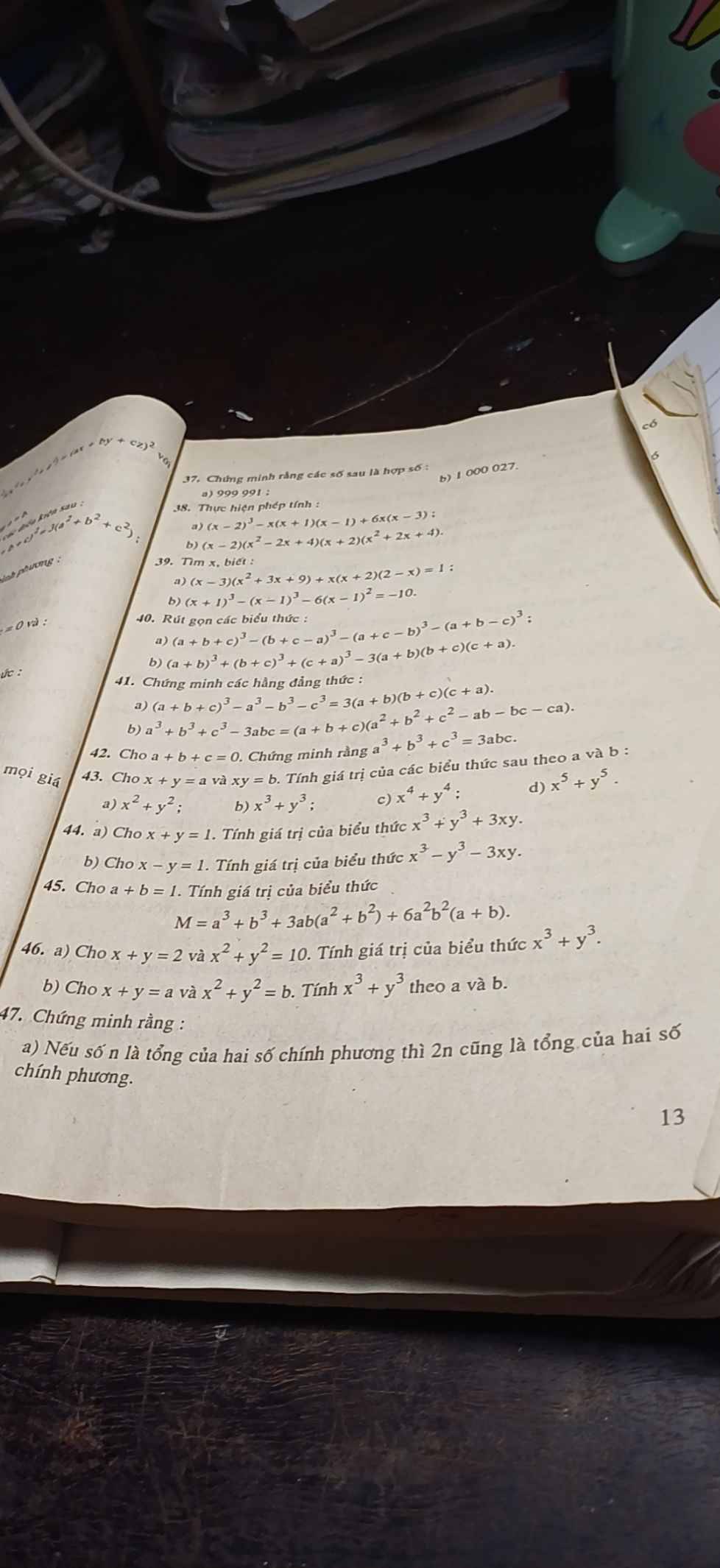Question

giúp e vs ạ bài nào cx đc

Answer 1

\(45.\)

\(M=a^3+b^3+3ab\left(a^2+b^2\right)+6a^2b^2\left(a+b\right)\)

\(=\left(a+b\right)\left(a^2-ab+b^2\right)+3ab\left[\left(a^2+2ab+b^2\right)-2ab\right]+6a^2b^2\left(a+b\right)\)

\(=\left(a+b\right)\left(a^2-ab+b^2\right)+3ab\left[\left(a+b\right)^2-2ab\right]+6a^2b^2\left(a+b\right)\)

\(=a^2-ab+b^2+3ab\left(1-2ab\right)+6a^2b^2\)

\(=a^2-ab+b^2+3ab-6a^2b^2+6a^2b^2\)

\(=a^2+2ab+b^2\)

\(=\left(a+b\right)^2\)

\(=1^2\)

\(=1\).

Answer 2

42:

a^3+b^3+c^3-3abc

=(a+b)^3+c^3-3ab(a+b)-3bac

=(a+b+c)(a^2+2ab+b^2-ac-bc+c^2)-3ab(a+b+c)

=0

=>a^3+b^3+c^3=3abc

44:

a: x^3+y^3+3xy

=(x+y)^3-3xy(x+y)+3xy

=1^3-3xy+3xy=1

b: x^3-y^3-3xy

=(x-y)^3+3xy(x-y)-3xy

=1^3+3xy-3xy=1

Answer 3

Bài 39:

a. 

PT $\Leftrightarrow x^3-3^3+x(2^2-x^2)=1$
$\Leftrightarrow x^3-27+4x-x^3=1$

$\Leftrightarrow 4x-27=1$

$\Leftrightarrow 4x=28$

$\Leftrightarrow x=7$
b.

PT $\Leftrightarrow x^3+3x^2+3x+1-(x^3-3x^2+3x-1)-6(x^2-2x+1)=-10$
$\Leftrightarrow 6x^2+2-6x^2+12x-6=-10$

$\Leftrightarrow 12x-4=-10$

$\Leftrightarroq 12x=-6$

$\Leftrightarrow x=\frac{-1}{2}$

Answer 4

Bài 40:

Sử dụng đẳng thức quen thuộc:

$(x+y+z)^3=x^3+y^3+z^3+3(x+y)(y+z)(x+z)$

------------------------------

a. Gọi biểu thức là $A$

Đặt $b+c-a=x; a+c-b=y, a+b-c=z$. Khi đó:

$A=(x+y+z)^3-x^3-y^3-z^3$

$=3(x+y)(y+z)(x+z)=3(2c)(2a)(2b)=24abc$

b.

$B=a^3+b^3+3ab(a+b)+b^3+c^3+3bc(b+c)+c^3+a^3+3ca(c+a)-3(a+b)(b+c)(c+a)$
$=2(a^3+b^3+c^3)+3[ab(a+b)+bc(b+c)+ca(c+a)]-3(a+b)(b+c)(c+a)$

$=2(a^3+b^3+c^3)-6abc+3[ab(a+b+c)+bc(b+c+a)+ca(c+a)]-3(a+b)(b+c)(c+a)$
$=2(a^3+b^3+c^3-3abc)+3[(a+b+c)(ab+bc)+ca(c+a)]-3(a+b)(b+c)(c+a)$

$=2(a^3+b^3+c^3-3abc)+3(c+a)[b(a+b+c)+ac]-3(a+b)(b+c)(c+a)$

$=2(a^3+b^3+c^3-3abc)+3(c+a)(a+b)(b+c)-3(a+b)(b+c)(c+a)$

$=2(a^3+b^3+c^3-3abc)$

Answer 5

Bài 41:

a.

$(a+b+c)^3-a^3-b^3-c^3=[(a+b)+c]^3-a^3-b^3-c^3$
$=(a+b)^3+c^3+3(a+b)c(a+b+c)-a^3-b^3-c^3$

$=a^3+b^3+3ab(a+b)+c^3+3(a+b)c(a+b+c)-a^3-b^3-c^3$
$=3ab(a+b)+3(a+b)c(a+b+c)$

$=3(a+b)[ab+c(a+b+c)]=3(a+b)(c+a)(c+b)$ (đpcm)

b.

$a^3+b^3+c^3-3abc=(a+b)^3-3ab(a+b)+c^3-3abc$

$=(a+b)^3+c^3-3ab(a+b+c)$

$=(a+b+c)[(a+b)^2-c(a+b)+c^2]-3ab(a+b+c)$

$=(a+b+c)[(a+b)^2-c(a+b)+c^2-3ab]$

$=(a+b+c)(a^2+b^2+c^2-ab-bc-ac)$ (đpcm)

Answer 6

Bài 42:

Vì $a+b+c=0$ nên $a+b=-c$. Khi đó:

$a^3+b^3+c^3=(a+b)^3-3ab(a+b)+c^3$
$=(-c)^3-3ab(-c)+c^3=-c^3+3abc+c^3=3abc$ (đpcm)

Answer 7

Bài 43:
$x^2+y^2=(x+y)^2-2xy=a^2-2b$

$x^3+y^3=(x+y)^3-3xy(x+y)=a^3-3ab$

$x^4+y^4=(x^2+y^2)^2-2x^2y^2=(a^2-2b)^2-2b^2$

$x^5+y^5=(x^2+y^2)(x^3+y^3)-x^2y^2(x+y)$

$=(a^2-2b)(a^3-3ab)-b^2a=a^5-5a^3b+5ab^2$

Answer 8

Bài 44: 

Vì $x+y=1$ nên:

$x^3+y^3+3xy=x^3+y^3+3xy(x+y)=(x+y)^3=1^3=1$

Answer 9

Bài 45:

Vì $x-y=1$ nên $x^3-y^3-3xy=x^3-y^3-3xy(x-y)=x^3-3x^2y+3xy^2-y^3=(x-y)^3=1^3=1$

Answer 10

Bài 45:

$M=a^3+b^3+3ab(a^2+b^2)+6a^2b^2(a+b)$

$=(a+b)(a^2-ab+b^2)+3ab[(a+b)^2-2ab]+6a^2b^2$

$=a^2-ab+b^2+3ab(1-2ab)+6a^2b^2$
$=a^2-ab+b^2+3ab-6a^2b^2+6a^2b^2$

$=a^2+2ab+b^2=(a+b)^2=1^2=1$

Answer 11

Bài 46:

a. Ta có: $xy=\frac{(x+y)^2-x^2-y^2}{2}=\frac{2^2-10}{2}=-3$

$x^3+y^3=(x+y)^3-3xy(x+y)=8-6xy=8-6(-3)=26$

b.

$xy=\frac{(x+y)^2-(x^2+y^2)}{2}=\frac{a^2-b}{2}$

$x^3+y^3=(x+y)^3-3xy(x+y)=a^3-3xya=a^3-3.\frac{a^2-b}{2}a$

$=\frac{3}{2}ab-\frac{1}{2}a^3$

 

Answer 12

Bài 47:

Đặt $n=a^2+b^2$ với $a^2,b^2$ là 2 số chính phương.

Khi đó:

$2n=2a^2+2b^2=(a^2+2ab+b^2)+(a^2-2ab+b^2)=(a+b)^2+(a-b)^2$ cũng là tổng của 2 số chính phương là $(a+b)^2$ và $(a-b)^2$ 

Ta có đpcm.