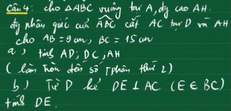Bài 2:
a: ta có: \(\left(x+3\right)^3-x\left(3x+1\right)^2+8x^3+1-3x^2=54\)
\(\Leftrightarrow x^3+9x^2+27x+27-x\left(9x^2+6x+1\right)+8x^3+1-3x^2-54=0\)
\(\Leftrightarrow9x^3+6x^2+27x-26-9x^3-6x^2-x=0\)
\(\Leftrightarrow26x=26\)
hay x=1
b: Ta có: \(\left(x-3\right)^3-\left(x^3-27\right)+6\left(x+1\right)^2+3x^2=-33\)
\(\Leftrightarrow x^3-9x^2+27x-27-x^3+27+6\left(x^2+2x+1\right)+3x^2+33=0\)
\(\Leftrightarrow-6x^2+27x+33+6x^2+12x+6=0\)
\(\Leftrightarrow39x=-39\)
hay x=-1
Bài 1:
a: \(x^2+4x+4=\left(x+2\right)^2\)
b: \(x^2-8x+16=\left(x-4\right)^2\)
c: \(\left(x+5\right)\left(x-5\right)=x^2-25\)
d: \(x^3+12x^2+48x+64=\left(x+4\right)^3\)
Bài 3:
a: \(A=1999\cdot2001=2000^2-1\)
mà \(2000^2-1< 2000^2\)
nên A<B
b: \(A=2011\cdot2013=2012^2-1\)
mà \(2012^2-1< 2012^2\)
nên A<B

 giúp e với! ! ! !
giúp e với! ! ! !


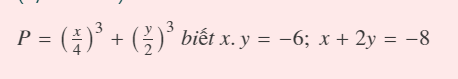








 giúp e với ạ e cảm ơn
giúp e với ạ e cảm ơn