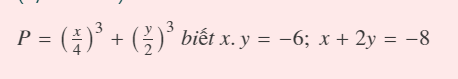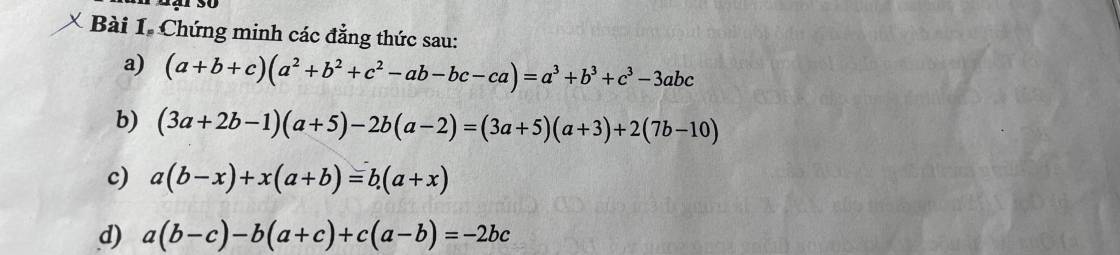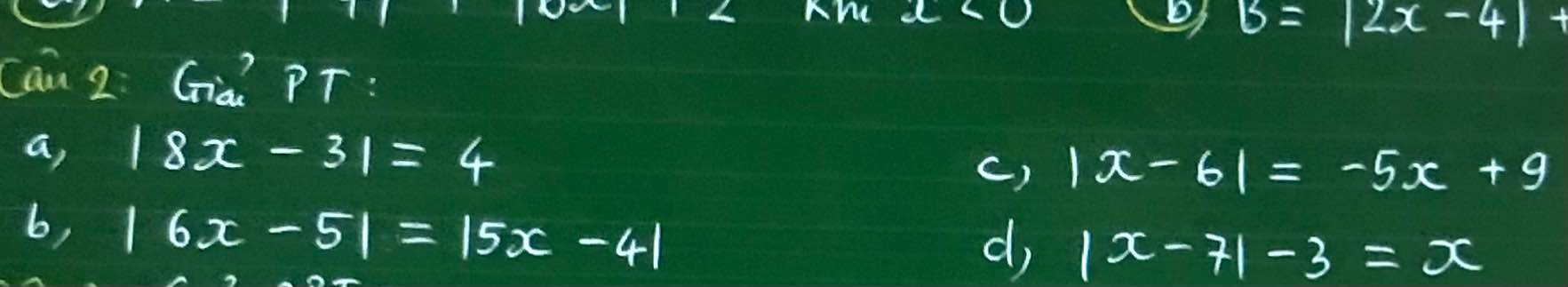theo đề ta có: \(x+y+z=0\Rightarrow\left(x+y+z\right)^2=0\)
\(\Rightarrow x^2+y^2+z^2+2\cdot\left(xy+yz+zx\right)=0\)
\(\Rightarrow x^2+y^2+z^2=-2\left(xy+yz+xz\right)\left(1\right)\)
ta co: \(x^3+y^3+z^3-3xyz=\left(x+y+z\right)\left(x^2+y^2+z^2-xy-yz-xz\right)\)
mà x + y + z = 0
\(\Rightarrow x^3+y^3+z^3-3xyz=0\Rightarrow x^3+y^3+z^3=3xyz\left(2\right)\)
a. VT = \(\left(x^2+y^2+z^2\right)^2=x^4+y^4+z^4+2\cdot\left(x^2y^2+y^2z^2+x^2z^2\right)\)
ta có: \(\left(xy+yz+zx\right)^2=\left(x^2y^2+y^2z^2+x^2z^2\right)+2xyz\cdot\left(x+y+z\right)\)
vì x+y+z=0 nên: \(\left(xy+yz+zx\right)^2=\left(x^2y^2+y^2z^2+x^2z^2\right)\)
từ (1) ta có: \(\left(x^2+y^2+z^2\right)^2=\left\lbrack-2\left(xy+yz+zx\right)^{}\right\rbrack^2\) (*)
\(=4\cdot\left(xy+yz+zx\right)^2=4\cdot\left(x^2y^2+y^2z^2+z^2x^2\right)\)
ta có: \(4\cdot\left(x^2y^2+y^2z^2+z^2x^2\right)=x^4+y^4+z^4+2\cdot\left(x^2y^2+y^2z^2+z^2x^2\right)\)
mà: \(2\cdot\left(x^2y^2+y^2z^2+z^2x^2\right)=x^4+y^4+z^4\)
thay vào (*) ta được:
\(\left(x^2+y^2+z^2\right)^2=\left(x^4+y^4+z^4\right)+2\cdot\left(x^2y^2+y^2z^2+z^2x^2\right)\)
\(=x^4+y^4+z^4+x^4+y^4+z^4=2\cdot\left(x^4+y^4+z^4\right)=VP\)
⇒ đpcm
b. \(VT=5\cdot\left(x^3+y^3+z^3\right)\left(x^2+y^2+z^2\right)\)
\(=5\cdot\left(3xyz\right)\left(x^2+y^2+z^2\right)\)
\(=15xyz\cdot\left(x^2+y^2+z^2\right)\) (3)
\(x+y+z=0\Rightarrow x+y=-z\)
\(x^5+y^5+z^5=x^5+y^5+\left\lbrack-\left(x+y\right)\right\rbrack^5=x^5+y^5-\left(x+y\right)^5\)
\(=x^5+y^5-\left(x^5+5y^4+10x^3y^2+10x^2y^3+5xy^4+y^5\right)\)
\(=-5x^4y-10x^3y^2-10x^2y^3-5xy^4\)
\(=-5xy\left(x^3+2x^2y+2xy^2+y^3\right)\)
\(=-5xy\left\lbrack x^3+y^3+2xy\left(x+y\right)\right\rbrack\)
\(=-5xy\left\lbrack\left(x+y\right)^3-3xy\left(x+Y\right)+2xy\left(x+y\right)\right\rbrack\)
\(=-5xy\left\lbrack\left(x+Y\right)^3-xy\left(x+y\right)\right\rbrack\)
\(=-5xy\left(x+Y\right)\left\lbrack\left(x+y\right)^2-xy\right\rbrack\)
vì x+y=-z nên ta có:
\(x^5+y^5+z^5=-5xy\left(-z\right)\left\lbrack\left(-z\right)^2-xy\right\rbrack=5xyz\left(x^2-zy\right)\)
mặt khác \(x+y=-z\Rightarrow\left(x+y\right)^2=z^2\Rightarrow x^2+y^2+2xy=z^2\)
\(x^2+y^2+z^2=x^2+y^2+\left(x+y\right)^2\)
\(=x^2+y^2+x^2+2xy+y^2=2\cdot\left(x^2+xy+y^2\right)\)
\(z^2-xy=\left(x+y\right)^2-xy=x^2+2xy+y^2-xy=x^2+xy+y^2\)
vậy \(x^5+y^5+z^5=5xyz\cdot\left(x^2+xy+y^2\right)=\frac52xyz\left(x^2+y^2+z^2\right)\)
\(\Rightarrow2\cdot\left(x^5+y^5+z^5\right)=5xyz\left(x^2+y^2+z^2\right)\)
⇒ \(6\cdot\left(x^5+y^5+z^5\right)=15xyz\left(x^2+y^2+z^2\right)\) (4)
từ (3) và (4) ⇒ VT = VP
câu c: phần này đã được chứng minh nằm trong câu b nha bạn