1: \(\left(2x+1\right)^2-4x^2+2x-2=0\)
=>\(4x^2+4x+1-4x^2+2x-2=0\)
=>6x-1=0
=>6x=1
=>\(x=\dfrac{1}{6}\)
3: \(\left(x-2\right)\left(x+2\right)-\left(x+3\right)^2-2x-5=0\)
=>\(x^2-4-x^2-6x-9-2x-5=0\)
=>-8x-18=0
=>8x=-18
=>\(x=-\dfrac{18}{8}=-\dfrac{9}{4}\)
5: \(\left(2x-1\right)\left(2x+1\right)-\left(2x-2\right)^2-2x=0\)
=>\(4x^2-1-\left(4x^2-8x+4\right)-2x=0\)
=>\(4x^2-2x-1-4x^2+8x-4=0\)
=>6x-5=0
=>6x=5
=>\(x=\dfrac{5}{6}\)
11: \(25x^2-10x+1=0\)
=>\(\left(5x\right)^2-2\cdot5x\cdot1+1^2=0\)
=>\(\left(5x-1\right)^2=0\)
=>5x-1=0
=>5x=1
=>\(x=\dfrac{1}{5}\)
12: \(81x^2-36x+4=0\)
=>\(\left(9x\right)^2-2\cdot9x\cdot2+2^2=0\)
=>\(\left(9x-2\right)^2=0\)
=>9x-2=0
=>\(x=\dfrac{2}{9}\)
13: \(4x^2-25=0\)
=>\(4x^2=25\)
=>\(x^2=\dfrac{25}{4}\)
=>\(\left[{}\begin{matrix}x=\dfrac{5}{2}\\x=-\dfrac{5}{2}\end{matrix}\right.\)
14: \(16x^2-25=0\)
=>\(16x^2=25\)
=>\(x^2=\dfrac{25}{16}\)
=>\(\left[{}\begin{matrix}x=\dfrac{5}{4}\\x=-\dfrac{5}{4}\end{matrix}\right.\)

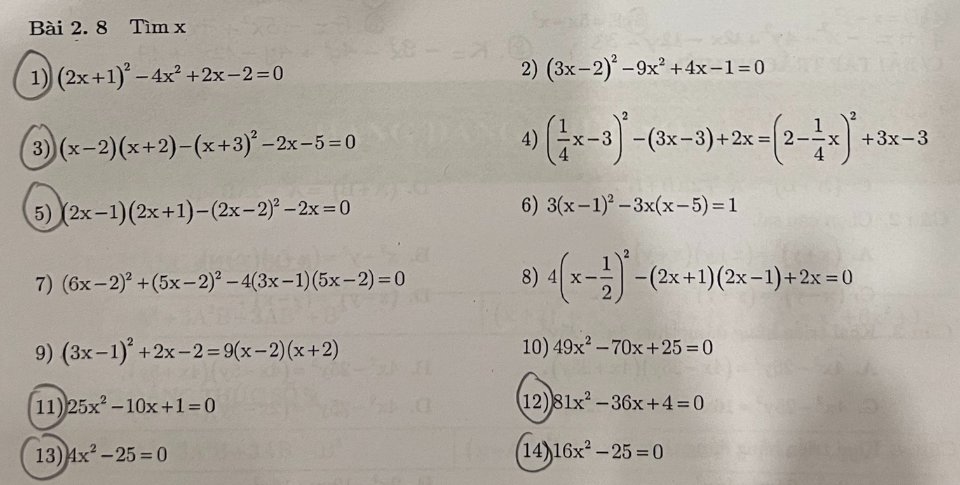 giúp e mấy câu khoanh tròn ạ
giúp e mấy câu khoanh tròn ạ